笛福赫尔曼密钥交换 DH KEY EXCHANGE

网上的文章通常喜欢直接抛出公式，证明起来也大多是已知结论来证明正确性的过程，比较学术和枯燥。 这篇文章顺着思考的方向再结合自己的理解，希望把笛福赫尔曼密钥交换讲明白。

首先需要知道两个最基本的概念：质数和合数

质数 Prime Number & 合数 Composite Number

在大于1的自然数中，除了1和它本身以外不再有其他因数，我们称之为「质数」 除了1和其本身外具有其他正因數的正整數，我们就称之为「合数」（用通俗的话讲就是如果某个数字能被分成大于 1 的等份，那么这个数就是合数）

好奇的人可能会想质数到底有多少个，它们能有多大，我们可以借助现代「质数螺旋」来看一下总体情况，首先将所有可能的数字以增长螺旋的形式给出，然后将所有质数做特殊标记，最后缩小来看大量数字的情况，就会看到一直持续到永远的质数规律，但是这个结构的一些重要规律现在仍然是未解的

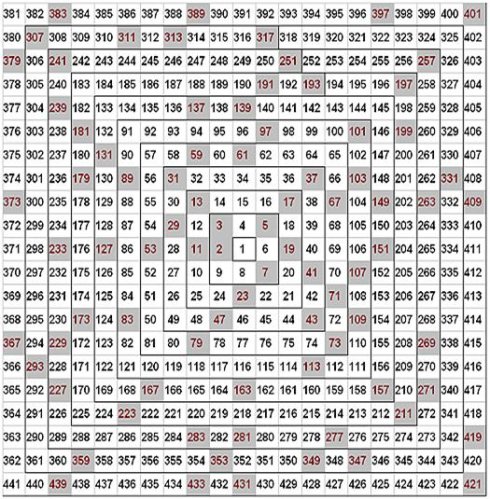
质数螺旋的链接可以查看：乌拉姆螺旋 - 维基百科，自由的百科全书

算数基本定理

早在公元前 300 年的古希腊，欧几里得就意识到所有的数都可以被分到这两个类别中，他首先意识到所有的数字都能不断进行除法，直到得到一组最小的不能进行除法的数字，根据定义，这些最小数字就是质数，所以所有的数字都是构建在这些质数之上的。 想象一个所有数字的集合，任意取一个合数进行分解，你将总能分解得到质数，欧几里得已经知道任何数字都能表示为一组质数，质数可以认为是积木，不管你选的是什么合数，它总能由质数之和来表示，这就是算数基本定理。 取任何数字（假设是 30），找到它可以分成的等份之合的所有质数（对于 30 来说就是 2、3、5），这个过程就是因数分解，欧几里得意识到，将这些质因数相乘特定次数，就能得到原数字（30 = 2^1 * 3^1 * 5^1），这些质因数可以认为是特殊的钥匙，因为任何数字有且只有一种质因数分解（没有其他质数组合相乘能得到 30 ），如果将每个数组看成是一个锁的话，那么每个锁的独特钥匙就是这个数字的质因数分解，就是任何两个锁的钥匙都不同，任何两个数的质因数分解也不同。 从最基础的数学定理中，就已经透出了些密码学的味道了~

颜色理论

随着计算机的发展，加密技术迅速发展，通常情况下，加密需要双方共享一个秘密的随机数，也就是密钥，那么未曾蒙面的两个人如果就密钥达成一致，而又不被第三个监听者知道呢？ 笛福和赫尔曼两人找到了一种巧妙的解决方式，我们可以以颜色作为例子，假设 Alice 和 Bob 需要共享一种颜色信息，但是有不能放第三方监听者 Eve 知道？ 该过程基于两点：① 混合两种颜色得到第三种颜色很容易 ②得到混合颜色后想在此基础上知道原来的两种颜色很难 那么这就是锁的原理，朝一个方向容易，朝反方向难，这种方法在数学上被称作单向函数 One-Way Function

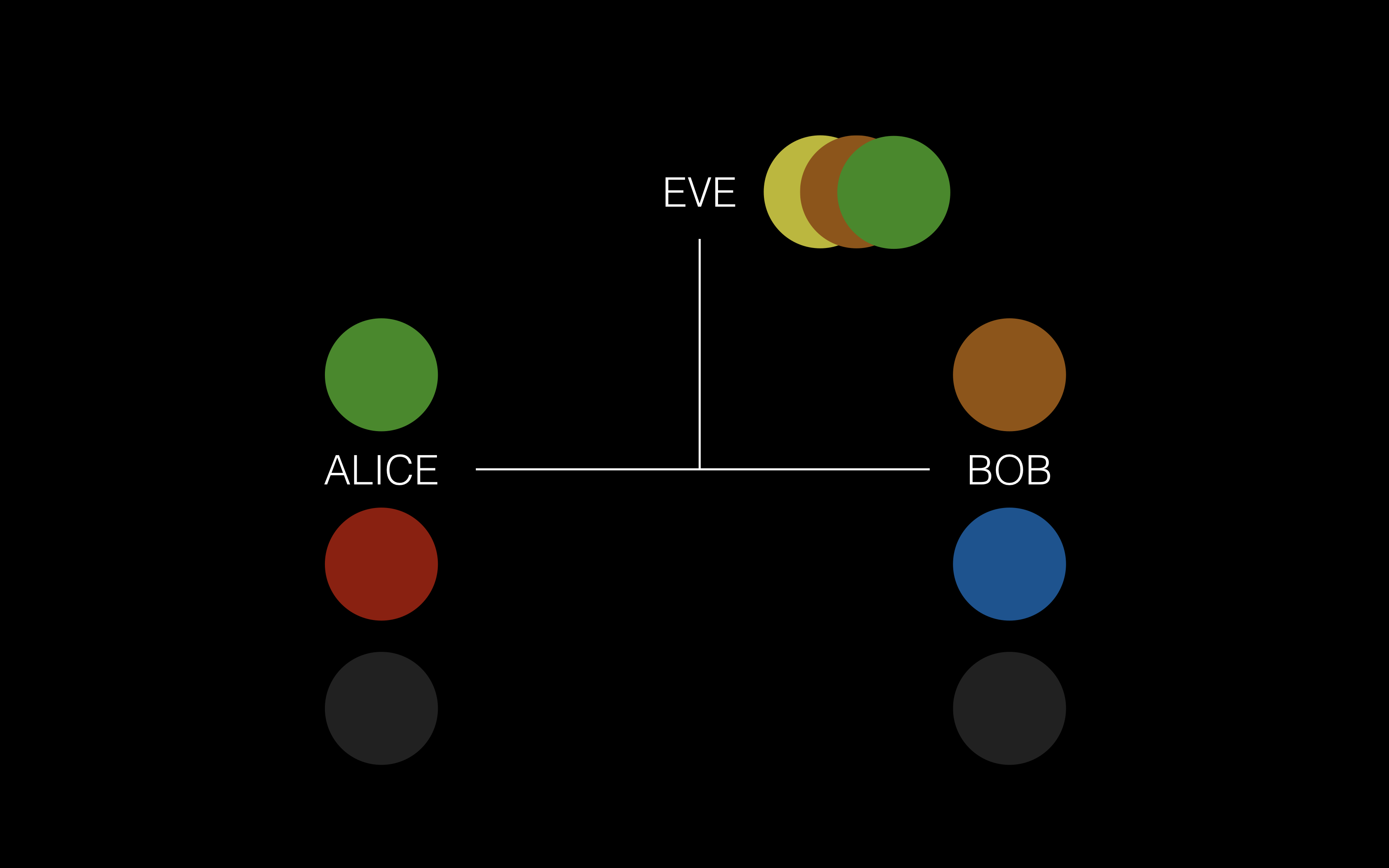
所以现在 Alice 和 Bob 应该这么做： ① 他们公开对某种颜色达成一致，这里假设是黄色 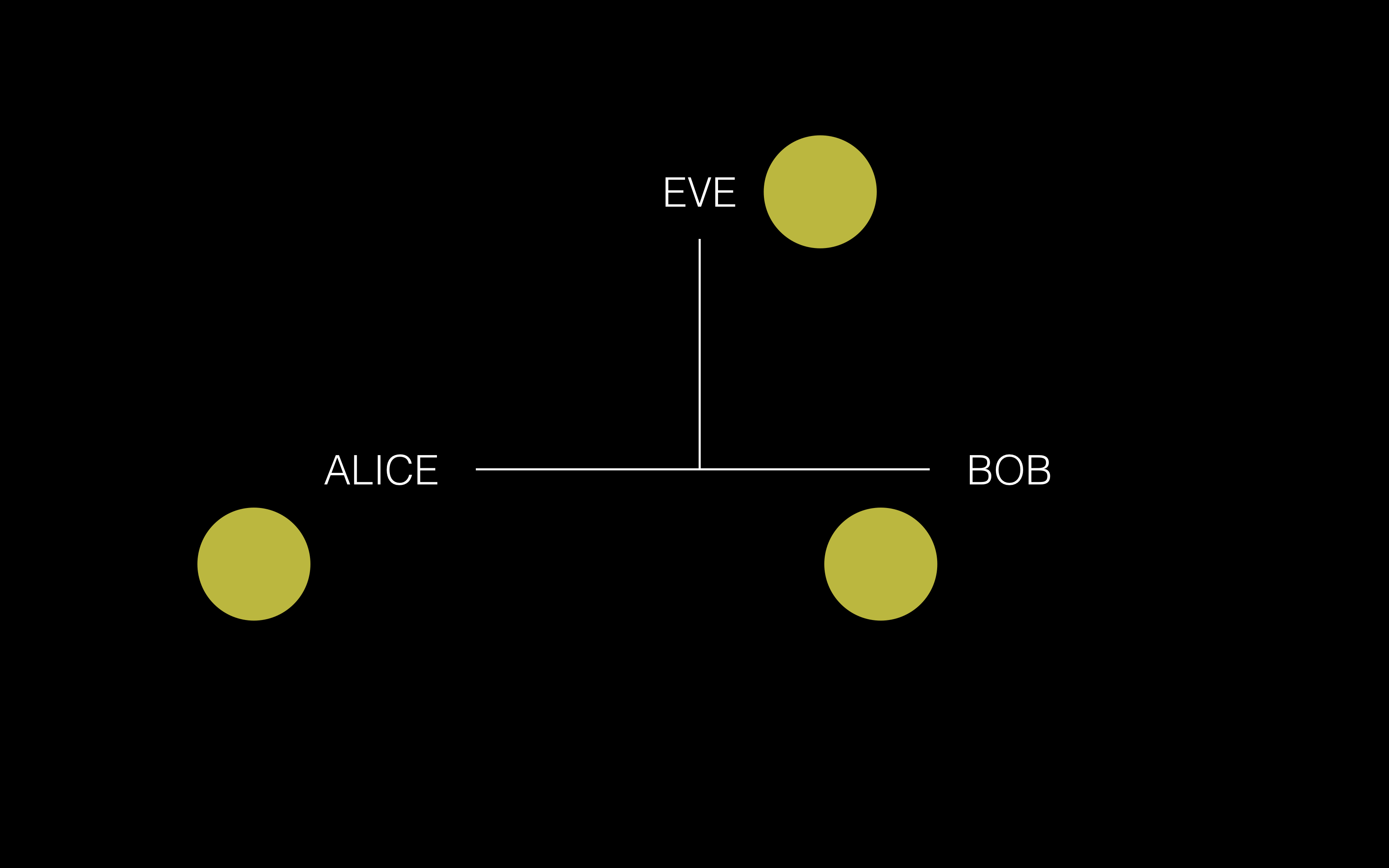② Alice 和 Bob 分别取自己的私有颜色，混合到公共的黄色中，从而隐藏掉自己的私有颜色，这里假设 Alice 取 红色，混合后得到橙色，Bob 取蓝色，混合后得到绿色 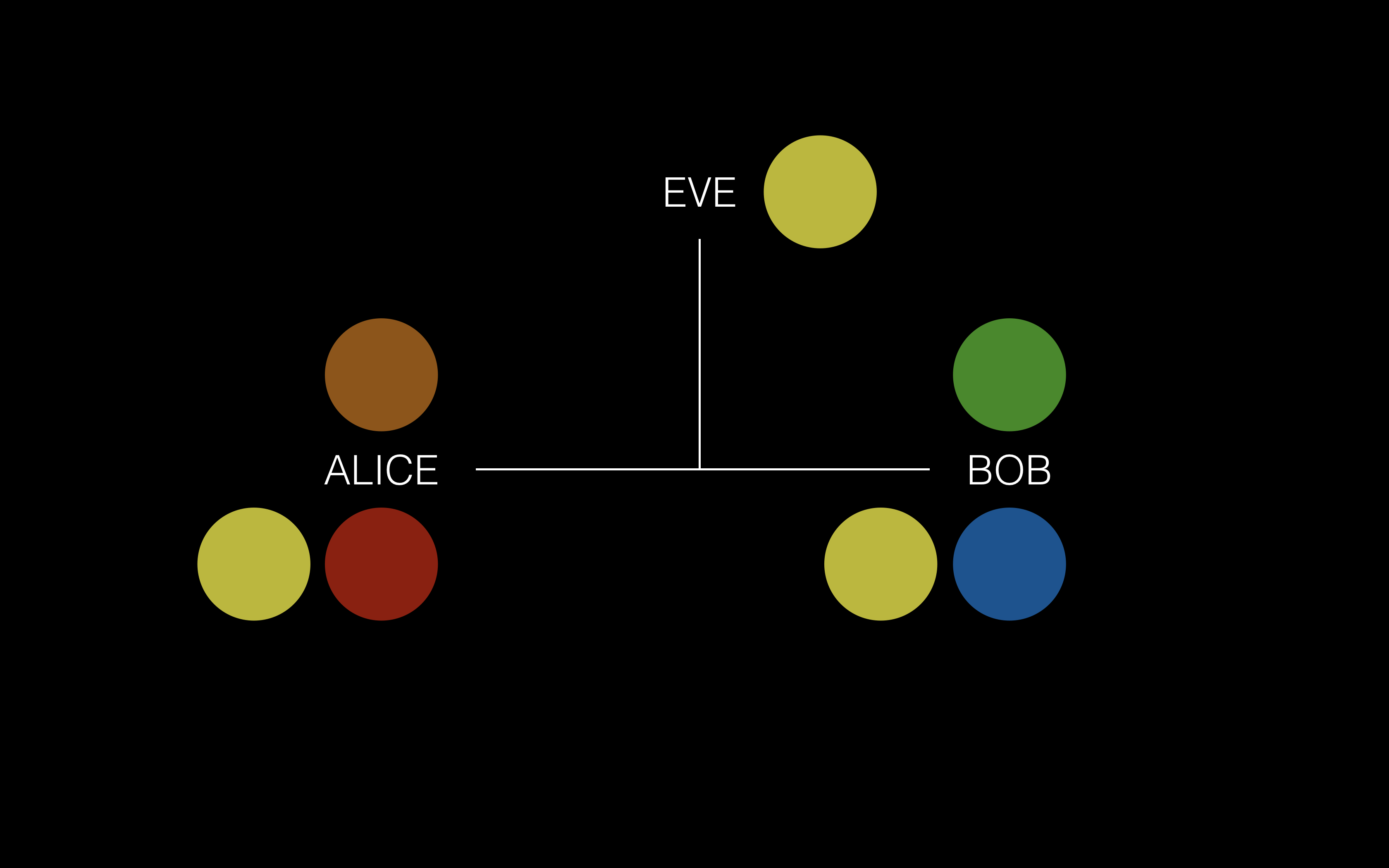③ Alice 和 Bob 分别将混合后的私有颜色发送给对方，以为是通过公共信道发送的，所以 Eve 会知道这两个混合色 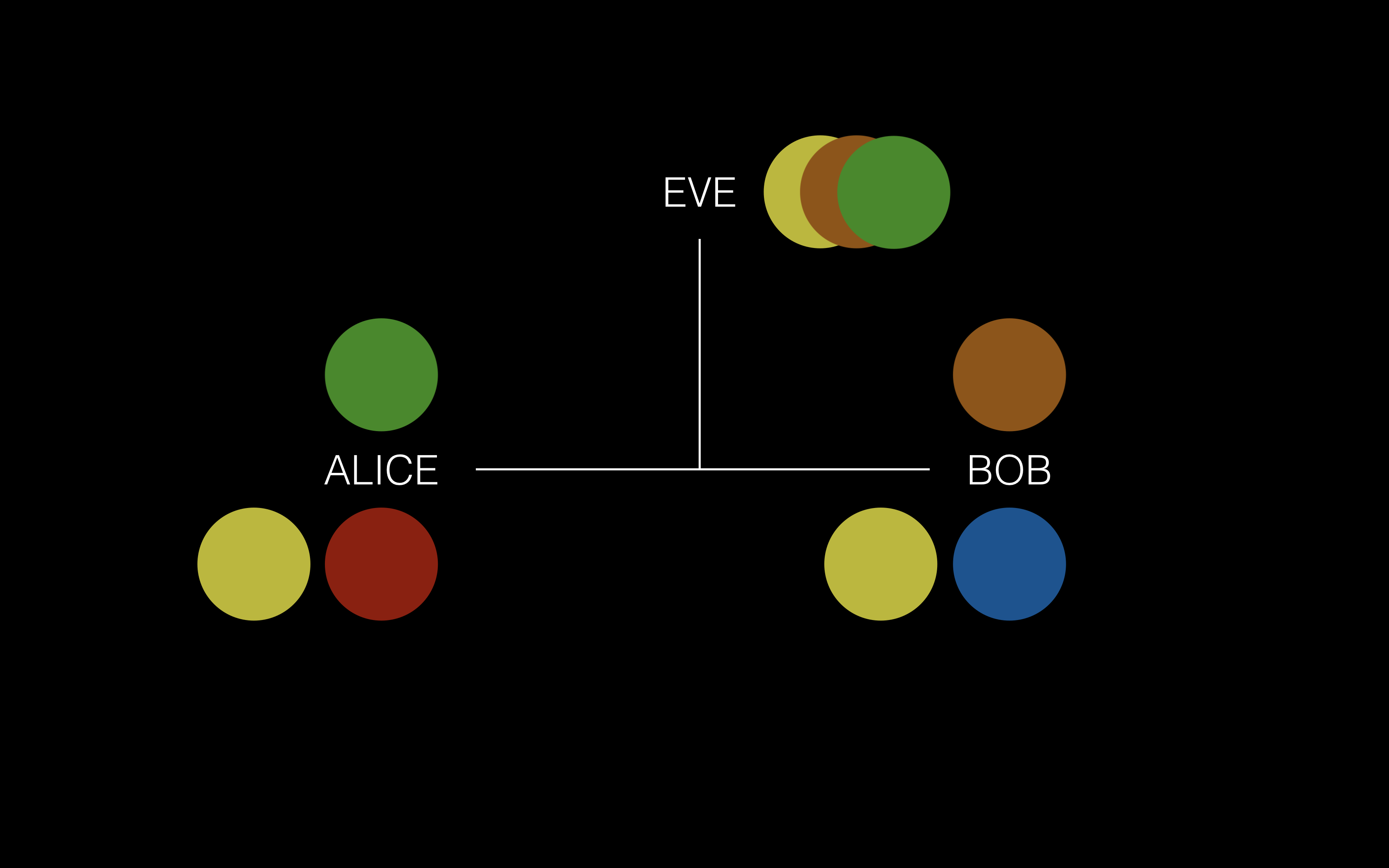④ Alice 和 Bob 将各自私有的颜色加入到接收到的混合颜色中，然后得到一种共享的秘密颜色，在这里 Alice 将自己私有的红色混合到接收到的绿色中， Bob 将自己私有的蓝色混合到接收到的橙色中，两个人会得到共同的颜色，此时因为 Eve 无法通过混合颜色分解出混合前的颜色，所以 Eve 无法知道 Alice 和 Bob 的私有颜色，因此 Eve 无法混合出正确的颜色

离散对数问题

要将上面这套理论应用于实践中，我们需要找到一个数学过程，该过程朝一个方向容易，反方向难。这里我们使用模运算，模运算用通俗的话来讲就是除法取余数的过程，比如 46 除以 12 得到余数 10，所以 46 mod 12 ≡ 10 下面我们考虑用质数来当模数，这里需要介绍另一个概念：生成元，我们拿质数 17 来举例子，我们可以很容易知道，除以 17 得到的余数只能是 0 -16 中的一个，3 是 17 的生成元，那么 3 具有的性质是：取 3 的 x 次方 mod17 的结果等可能的出现在 0 -16 中的任何数上

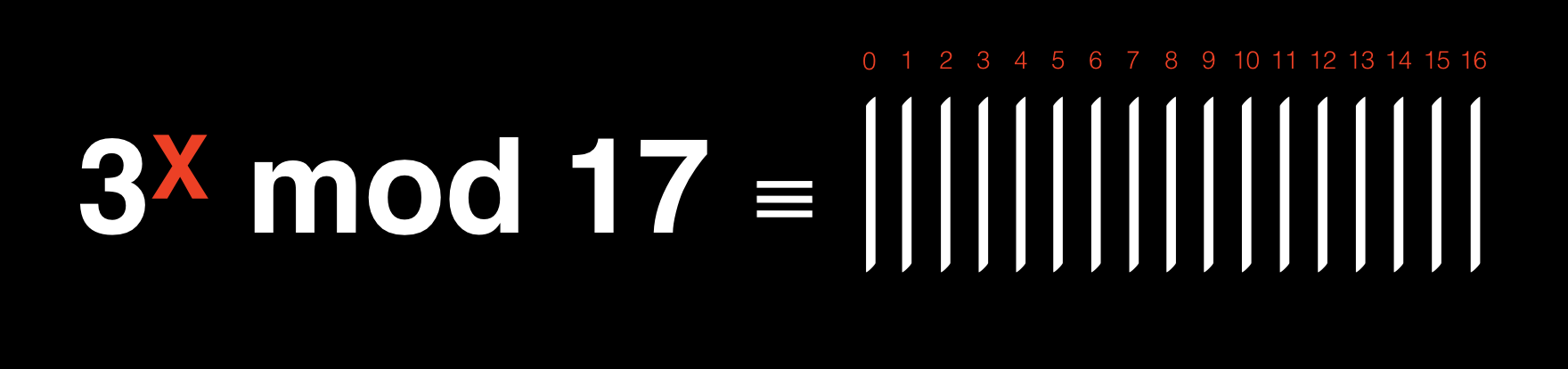
当给定一个 x 次方，我们很容易算出 mod 17 的余数，其过程无非就是乘法和除法运算，但是相反的过程就很难了，给定了最后的结果，想要求这个 x，我们只能采用试错的做法求出匹配的指数，当数字很小的时候，这个过程还是容易的，但是如果模数是长达数百位的质数，那么即使借助世界上最强大的计算机，要遍历所有可能也需要花上上千年的时间。单向函数的强度取决于反向过程所需要的时间

这个问题就被称作是离散对数问题。所以我们现在就有了单向函数。

DH KEY EXCHANGE

结合上面的颜色理论和离散对数问题，笛福赫尔曼密钥交换可以这么来实现： ① Alice 和 Bob 公开对质数和生成元达成一致，这里假设是 17 和 3

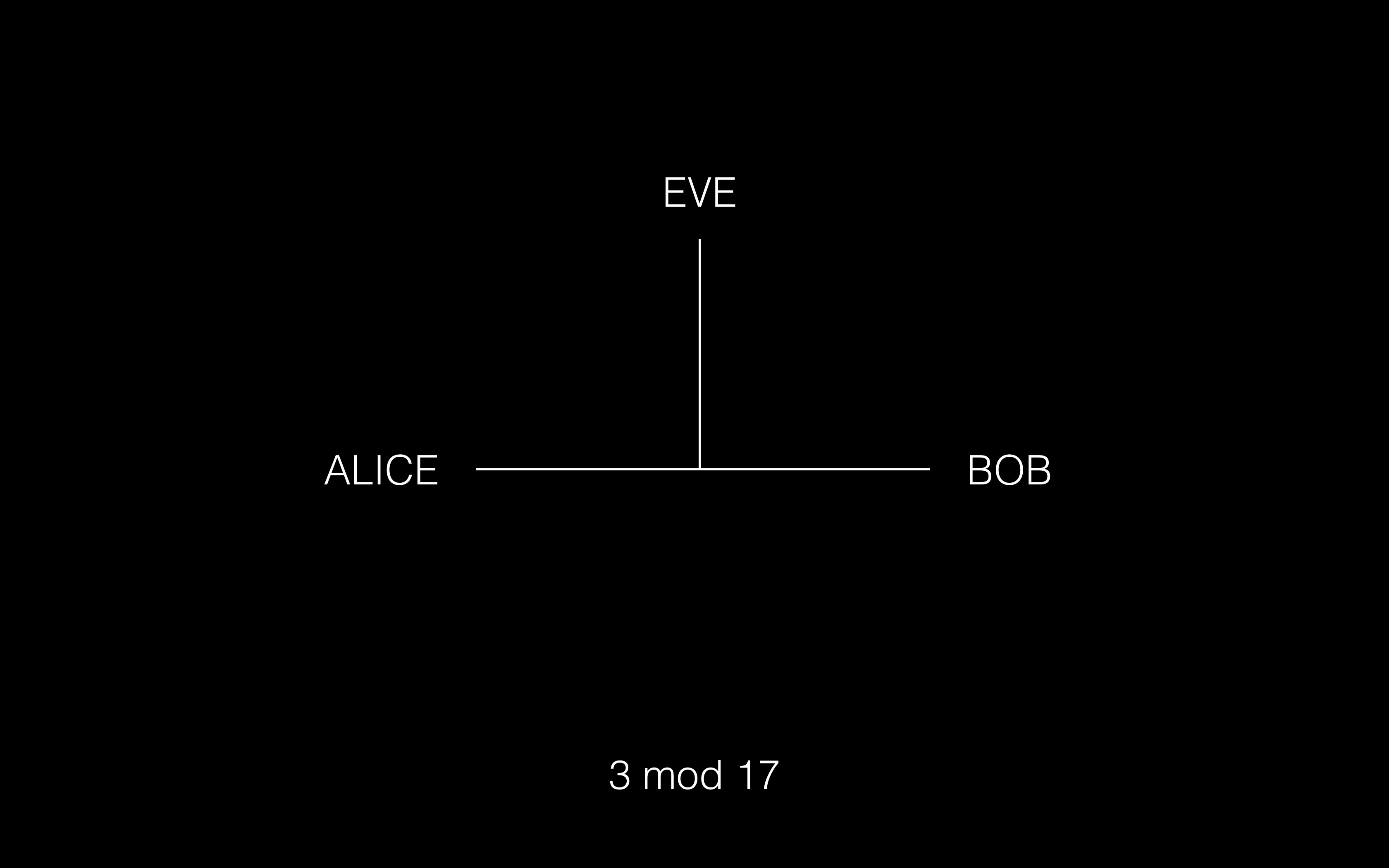
② Alice 选取自己的私有数字，这里假设 Alice 取 15，然后计算 3^15 mod 17 ≡ 6，然后将计算结果公开的发送给 Bob

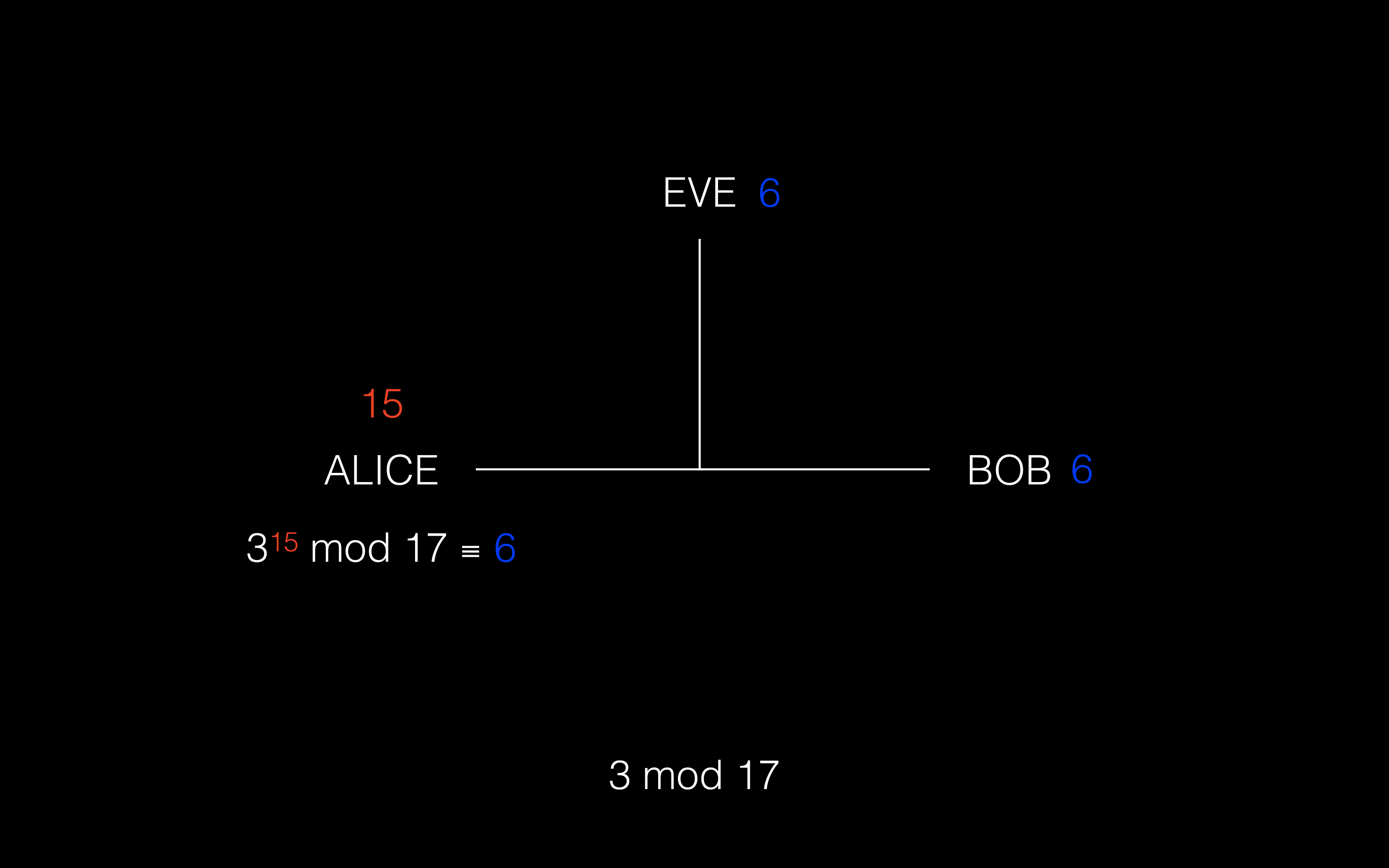
③ Bob 选取自己的私有数字，这里假设 Bob 取 13，然后计算 3^13 mod 17 ≡ 12，然后将计算结果公开的发送给 Alice

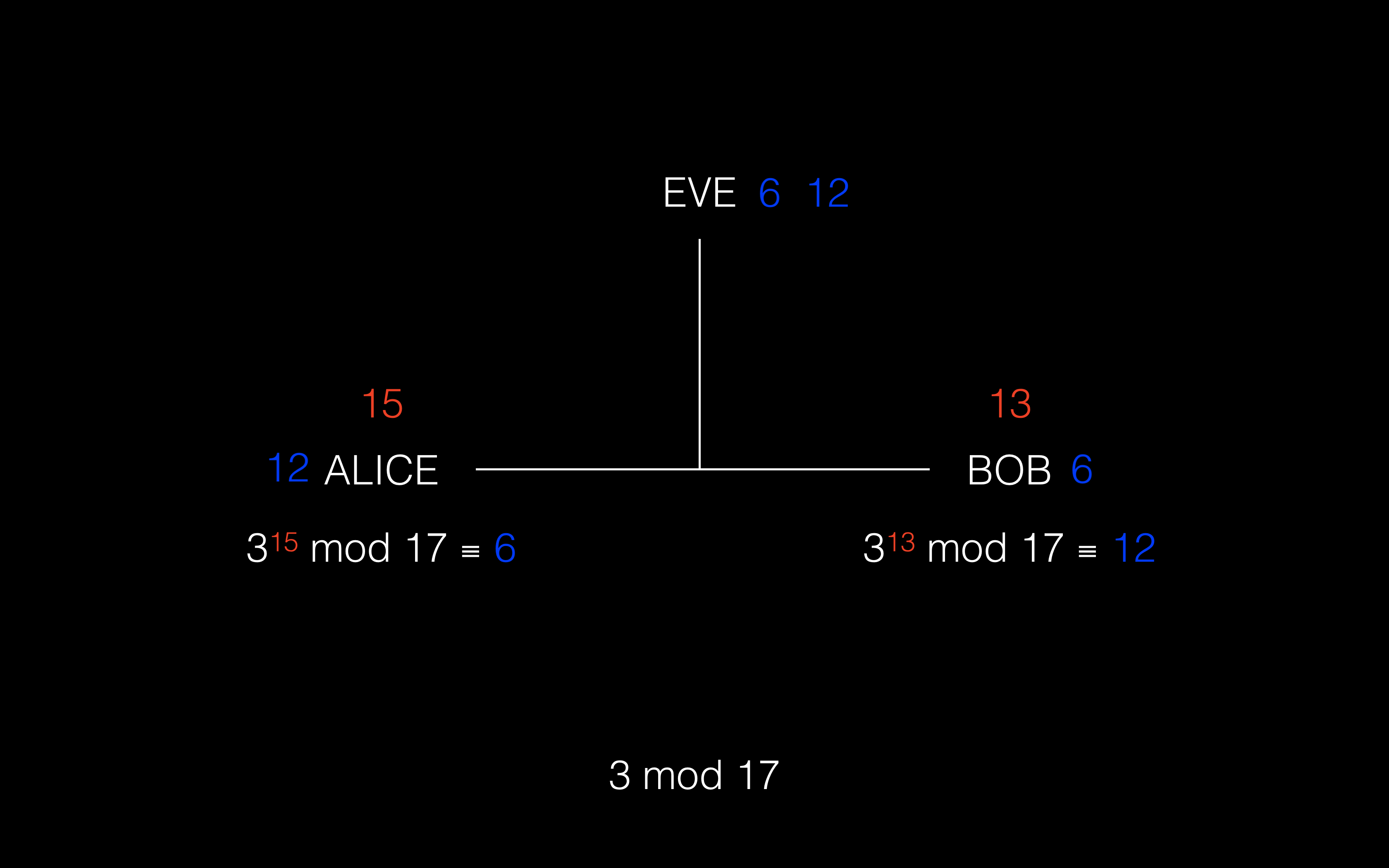
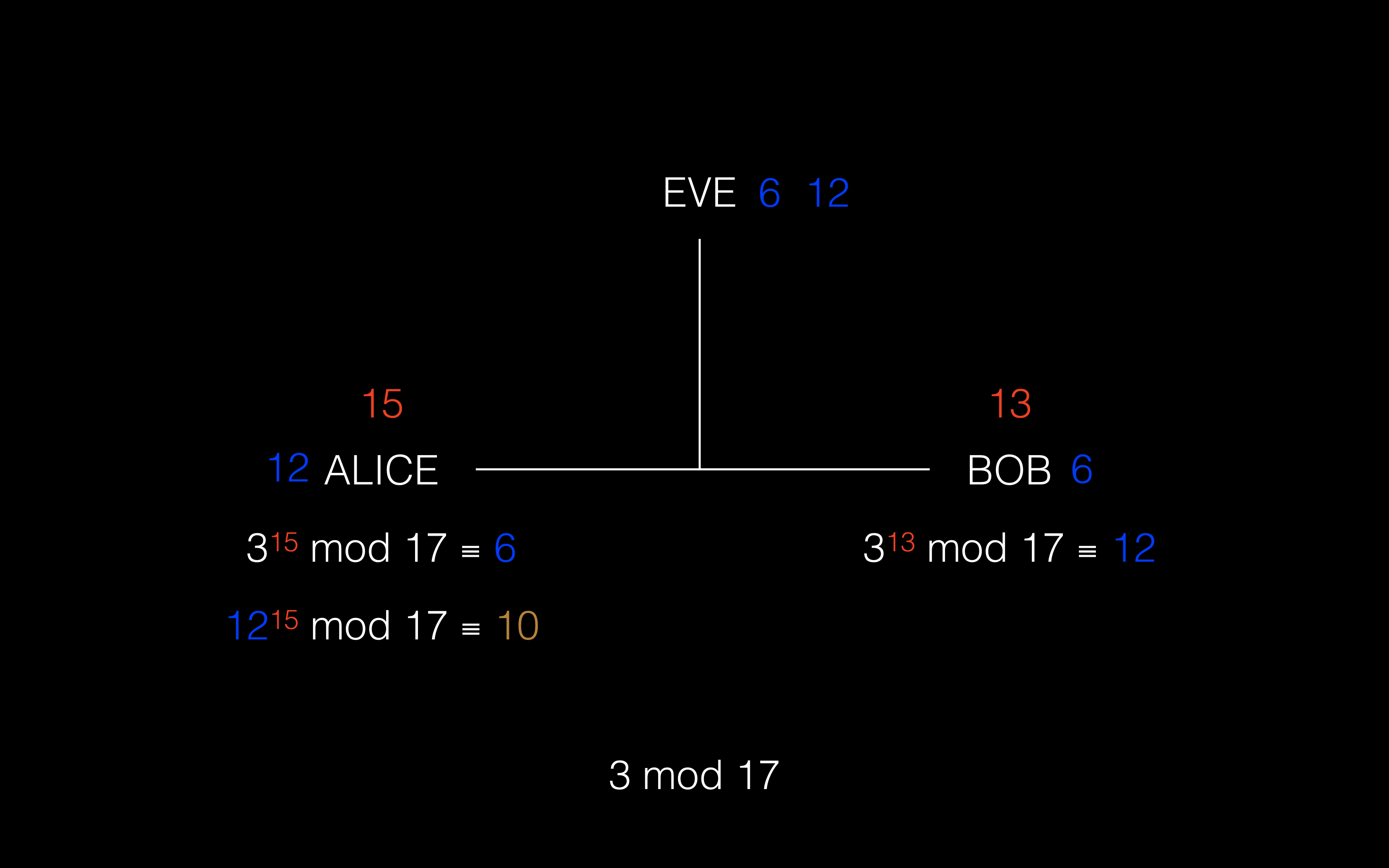
④ Alice 将 Bob 发送的公开结果 12 取他自己的私有数字次方以获得共享密钥，在这里就是 12^15 mod ≡ 10

⑤ Bob 将 Alice 发送的公开结果 6 取他自己的私有数字次方以获得同样的共享密钥，在这里就是 6^13 mod ≡ 10

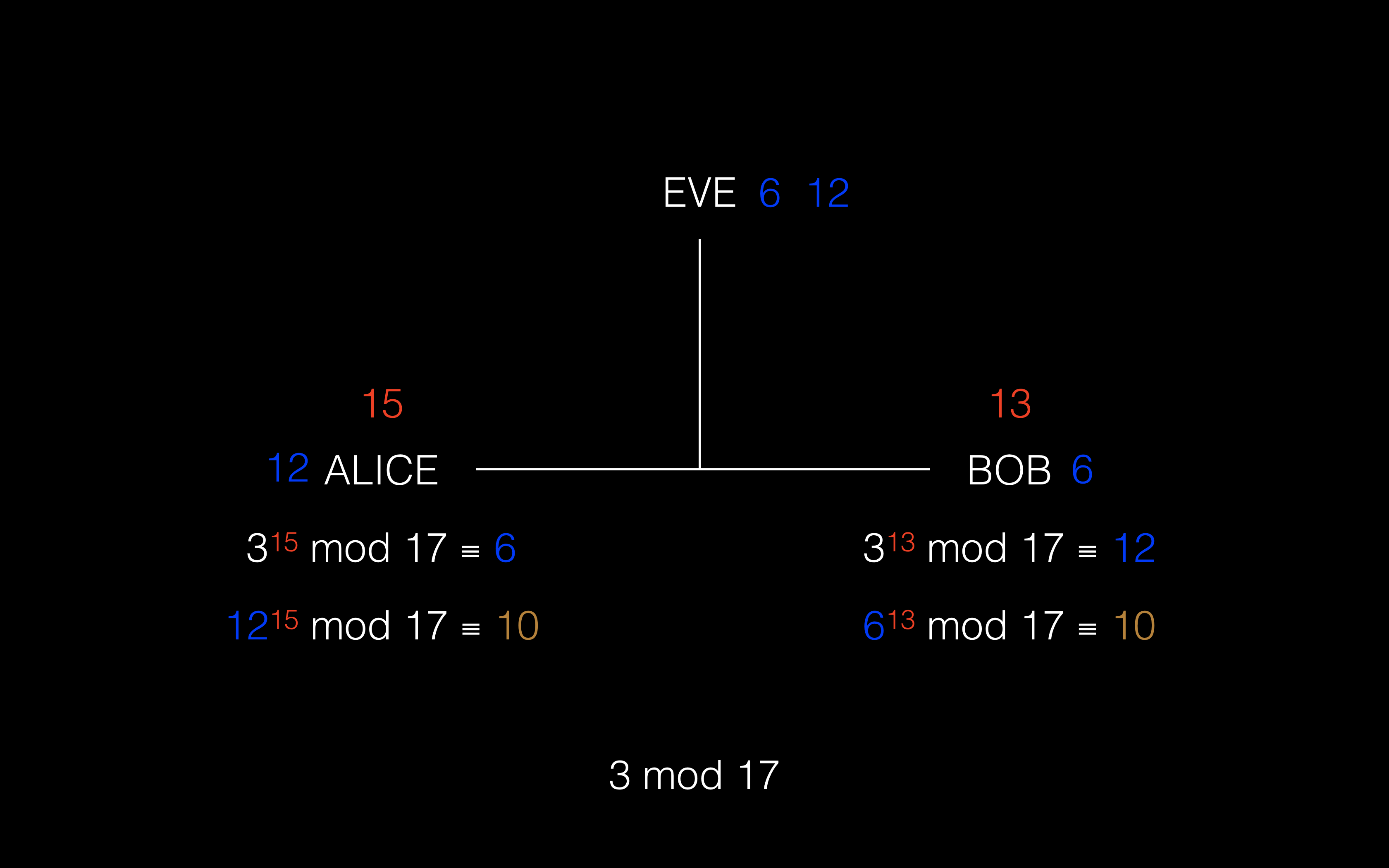
初看可能还不好理解，为什么两个运算会得到同样的结果，要说明这个过程我们需要借助一个模运算的运算规则： (a mod p)b mod p = ab mod p 有点类似于乘法分配律，也就是同样的 mod 运算可以提取出来放在最后统一进行。 那么 12^15 mod 17 中的 12 其实是 Bob 计算出来的，将计算过程代入： (3^13 mod 17)^15 mod 17 再结合上面说到的运算规则，式子可以变成： (3^13)^15 mod 17 同理，3^13 mod 17 -> (3^15 mod 17)^13 mod 17 -> (3^15)^13 mod 17 可以发现两个式子推算到最后的结果一定是一致的，共享密钥一定是生成元取两个人的私有数字次幂再求模得到的结果，不管 Alice 和 Bob 的私有数字取的是什么。

在整个过程中双方的私有数字都没有在信道中传输过，在妥善保管的情况下可以认为是绝对安全的，在不知道双方私有数字的情况下，Eve 将无法算出结果，因为离散对数问题使得知道模运算的结果很难得出对应的指数，当质数足够大的时候，在合理时间内几乎不可能破解，这就解决了密钥交换的问题。