RSA 理论的正向思考过程（二）
质因数分解
2000 多年前，欧几里得就证明了，每个数只要一种质因数分解，那么质因数的分解结果这可以考虑为一个密钥，因为质因数分解是个非常困难的问题，到底有都难？我找到一个有意思的网站，里面可以根据你的输入的数字来输出乘法和质因数分解求解的时间，当我输入 24 位数字的时候得到以下结果，看起来时间花费还可以：
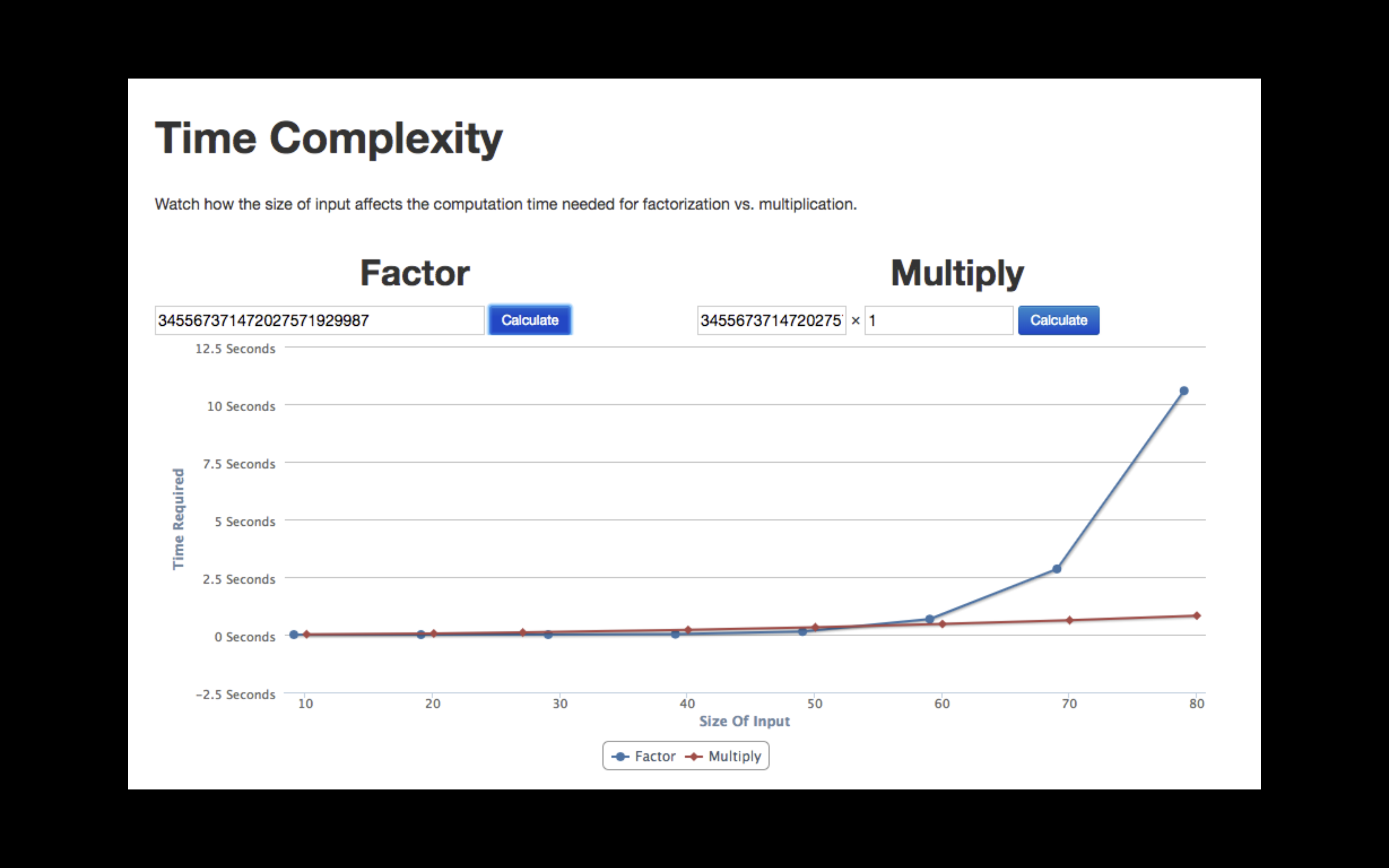当我将数字扩大到 100 位的时候，质因数分解的时间已经需要大概快八百万年了
所以质因数分解就是很难！那么我们就可以利用质因数分解来构造陷门：
① Alice 随机产生 150 为质数 p1，再随机生成位数差不多的质数 p2
② P1 * P2 = N 合数，N 将超过 300 位，整合做乘法很容易，用浏览器都能秒算，但是反过来求 N 的质因数分解 P1 P2 很难
③ 将 P1 * P2 隐藏或者销毁，然后将 N 公开，其他人如果想要通过 N 求解出 P1 或者 P2 是非常困难的
④ 接下来我们需要找到一个函数，这个函数的求解依赖于知道 N 的质因数分解，讲的更直白一点就是，我们需要一个函数，知道 N 的质因数分解后很容易求，但是不知道的话没法求解
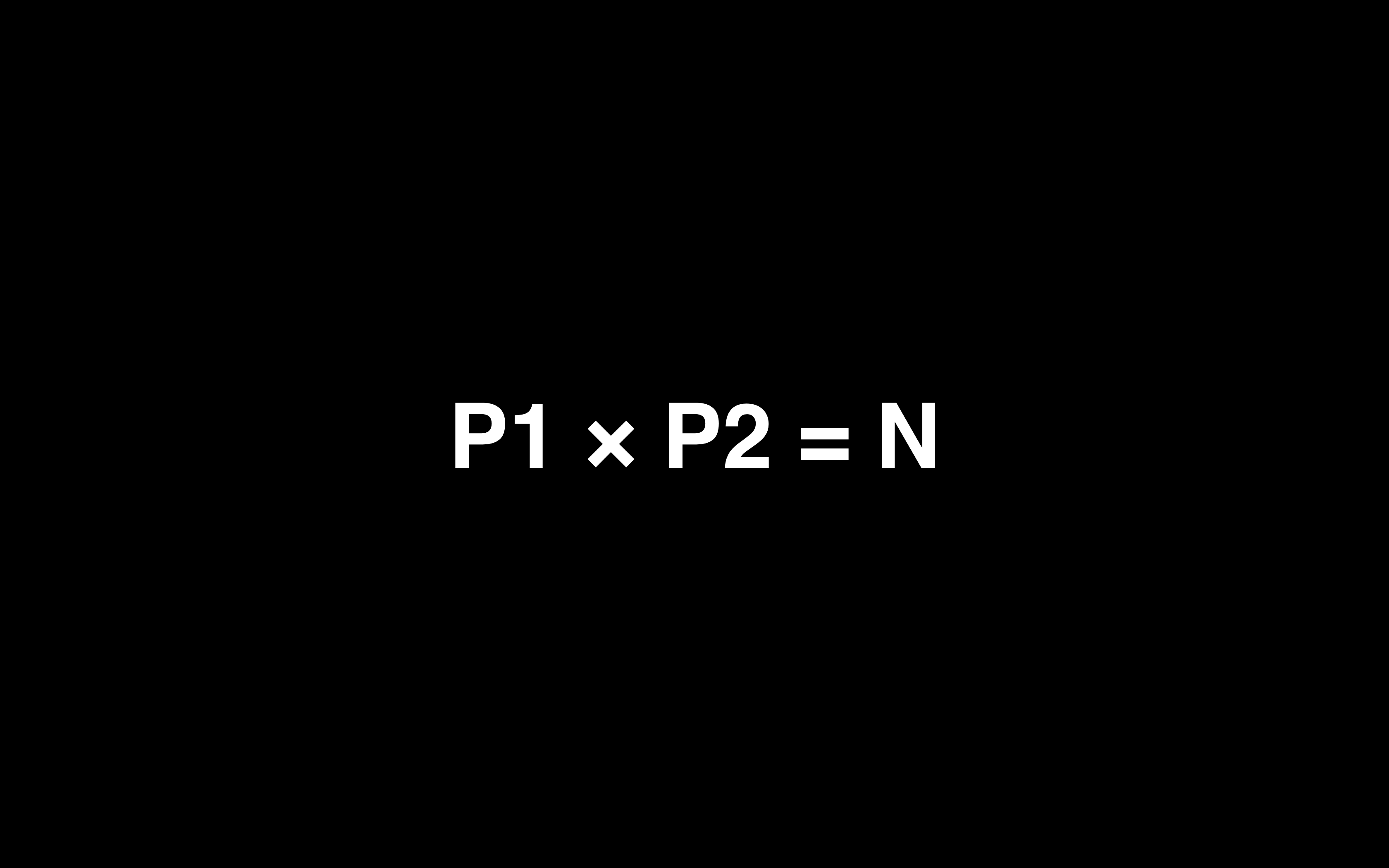
欧拉 φ 函数
为了解决上面的问题，我们需要运用到欧拉 φ 函数，这个函数衡量的是数的可分性。对于给定数字 N，函数输出的数字是有多少小于 N 的整数不与 N 具有任何公因数，以 φ(8) 来举个例子，我们考虑比 8 小的整数中与 8 互素的数的个数，一共有 1、3、5、7 这 4 个数，所以 φ(8) = 4
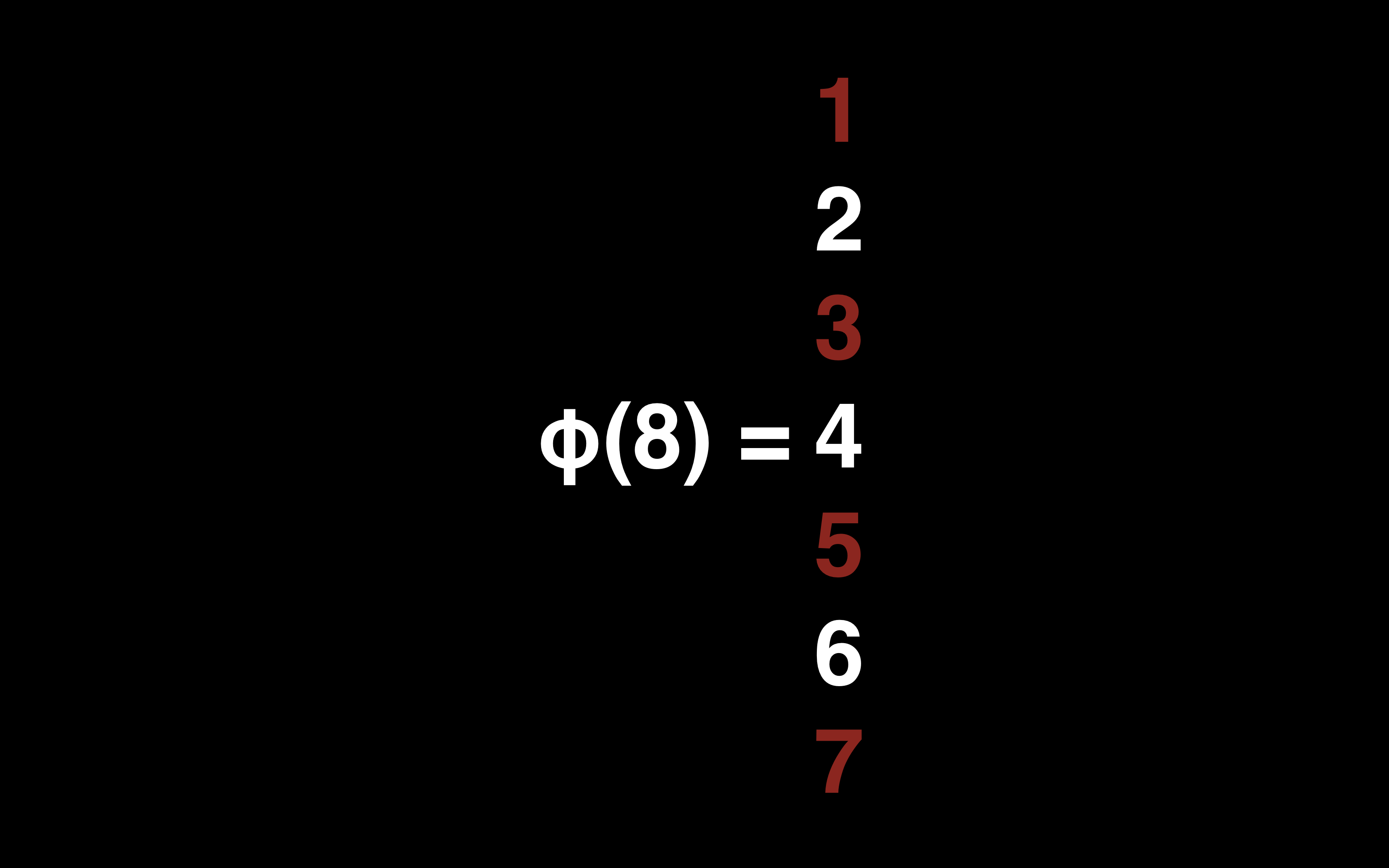有趣的是，计算欧拉 φ 函数很困难，除了一种情况，看下面的这张图：
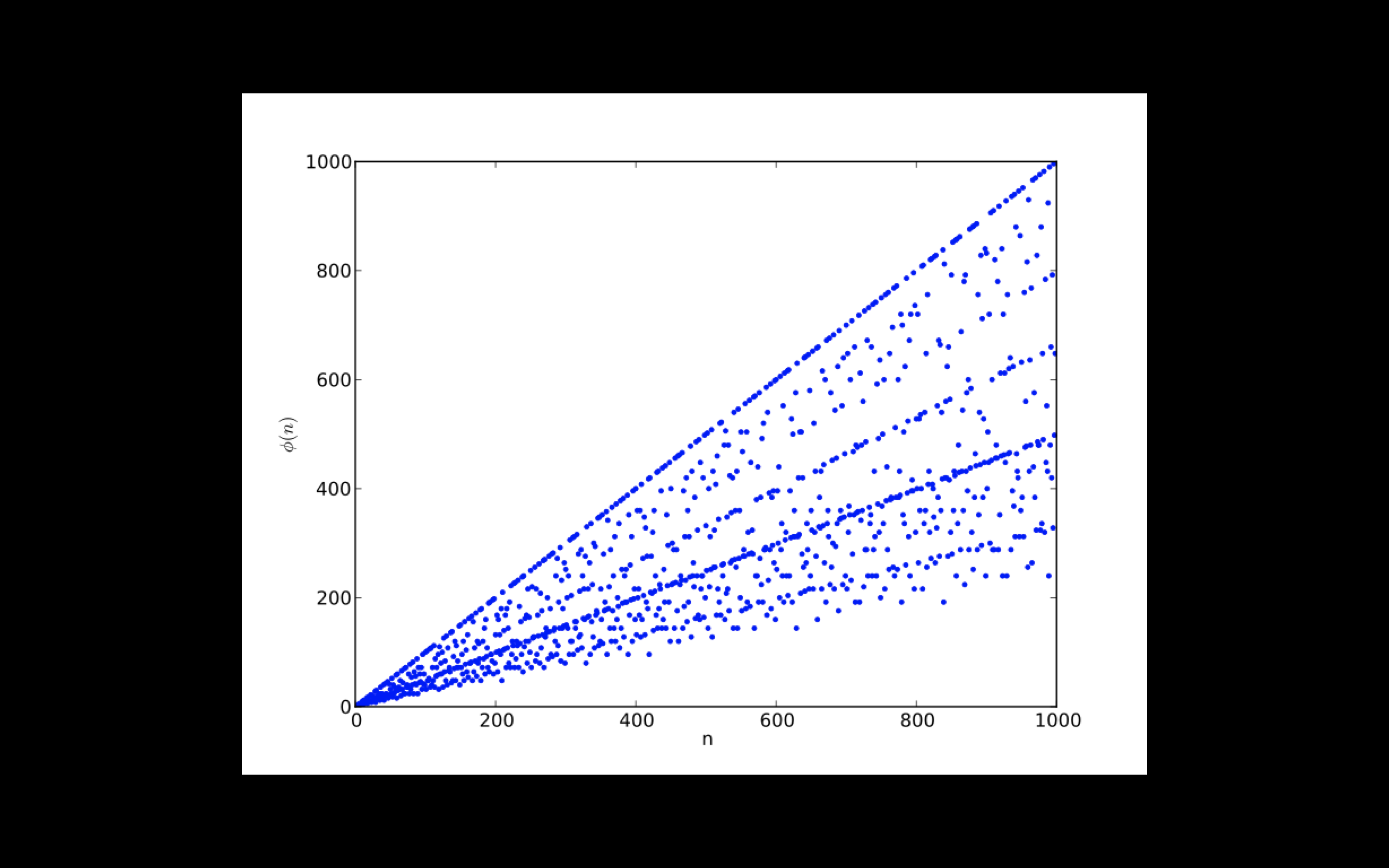这是 φ(n) 和 n 的一个图像，n 从1-1000，可以发现最上面那条直线表示了所有素数，因为素数没有大于 1 的因数，
根据 φ 的定义，我们也可以很容易知道 如果 p 是一个素数的话，那么比 p 小的正整数中和 p 互素的个数是 p - 1
所以对于任何素数 p，我们都能得到 φ(p) = p - 1
这里我们需要引入关于 φ 的一个乘法性质：
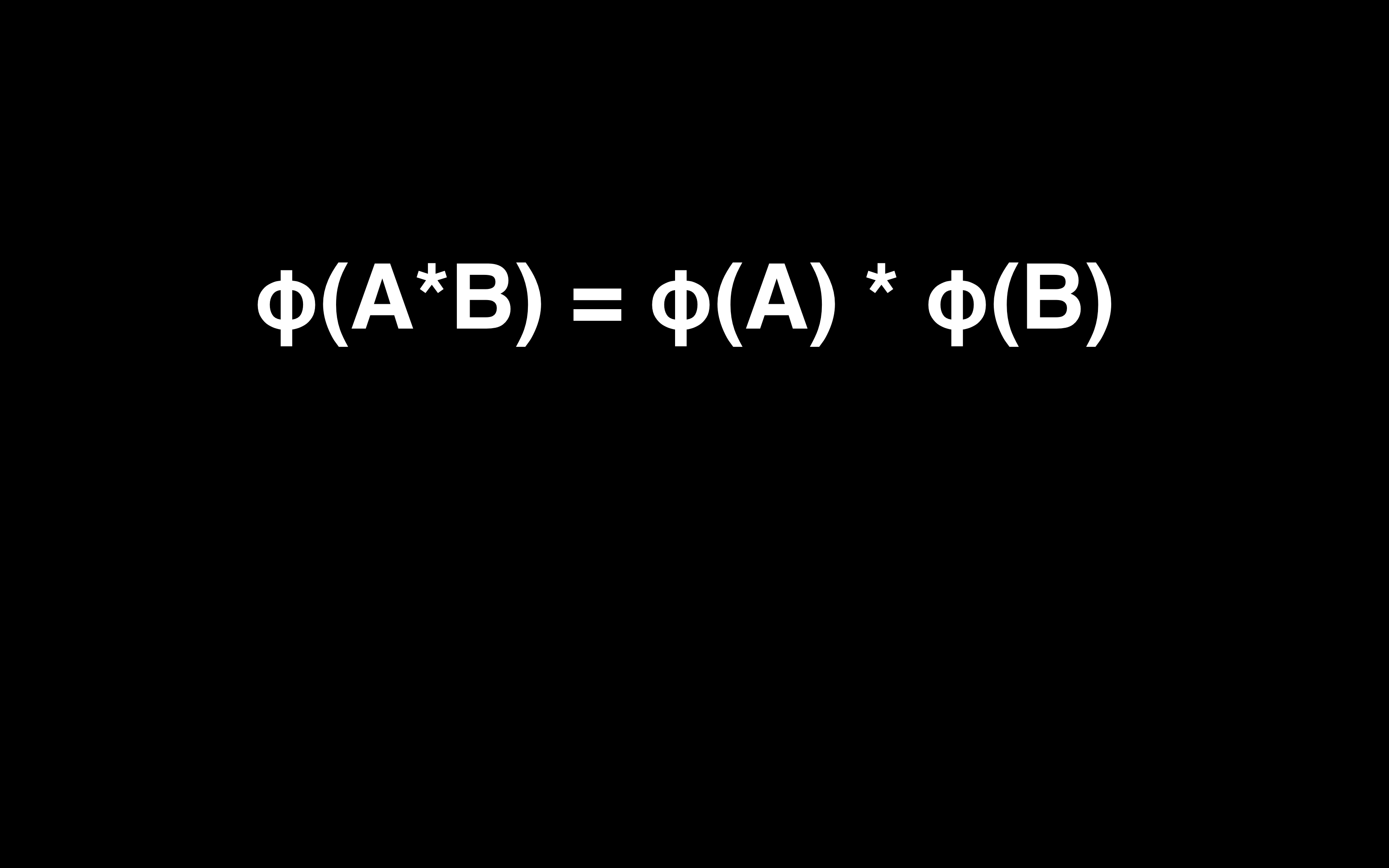如果知道数字 N 是两个质数 P1 和 P2 的乘积，那么 φ(N) = (P1 - 1) * (P2 - 1)
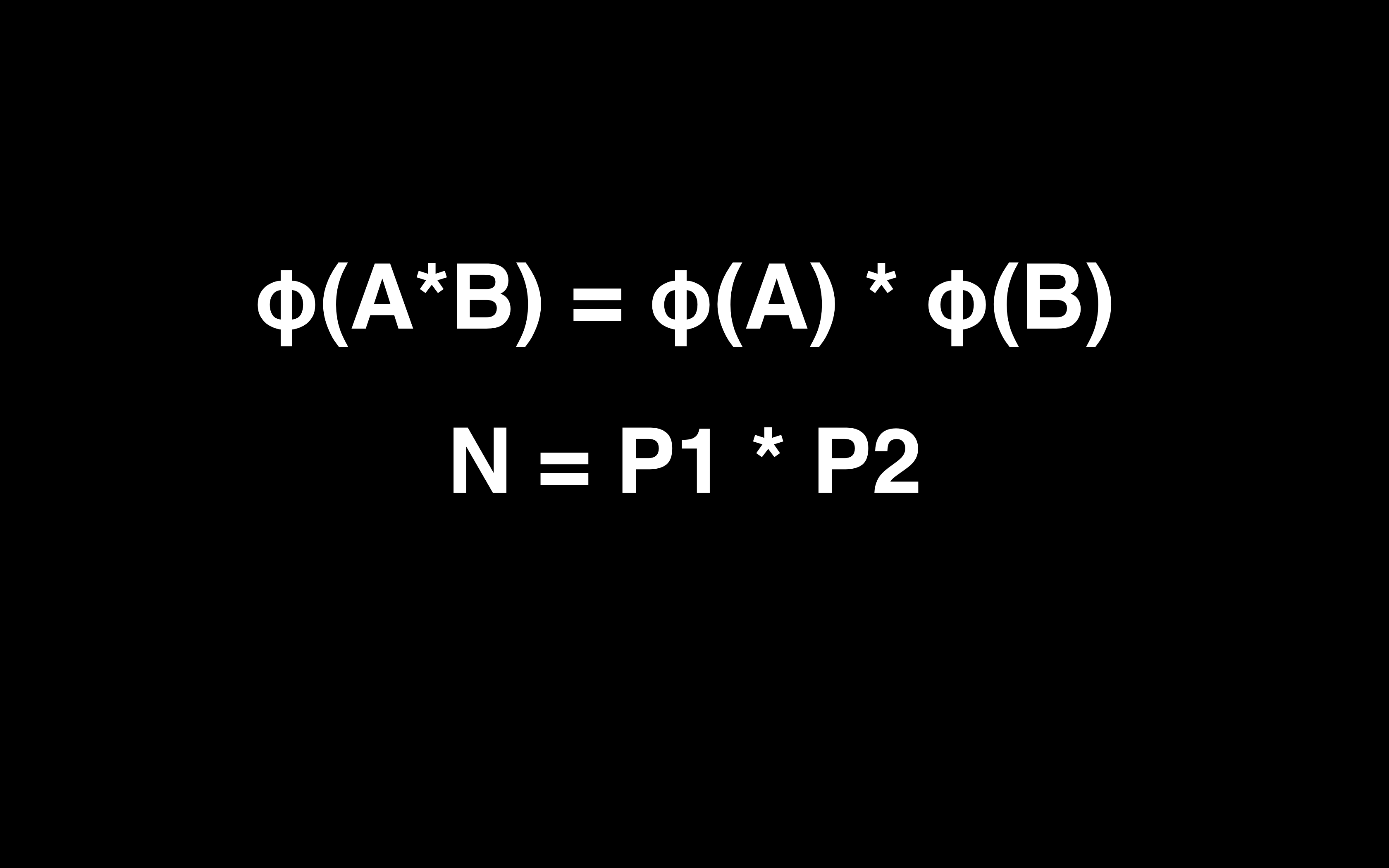
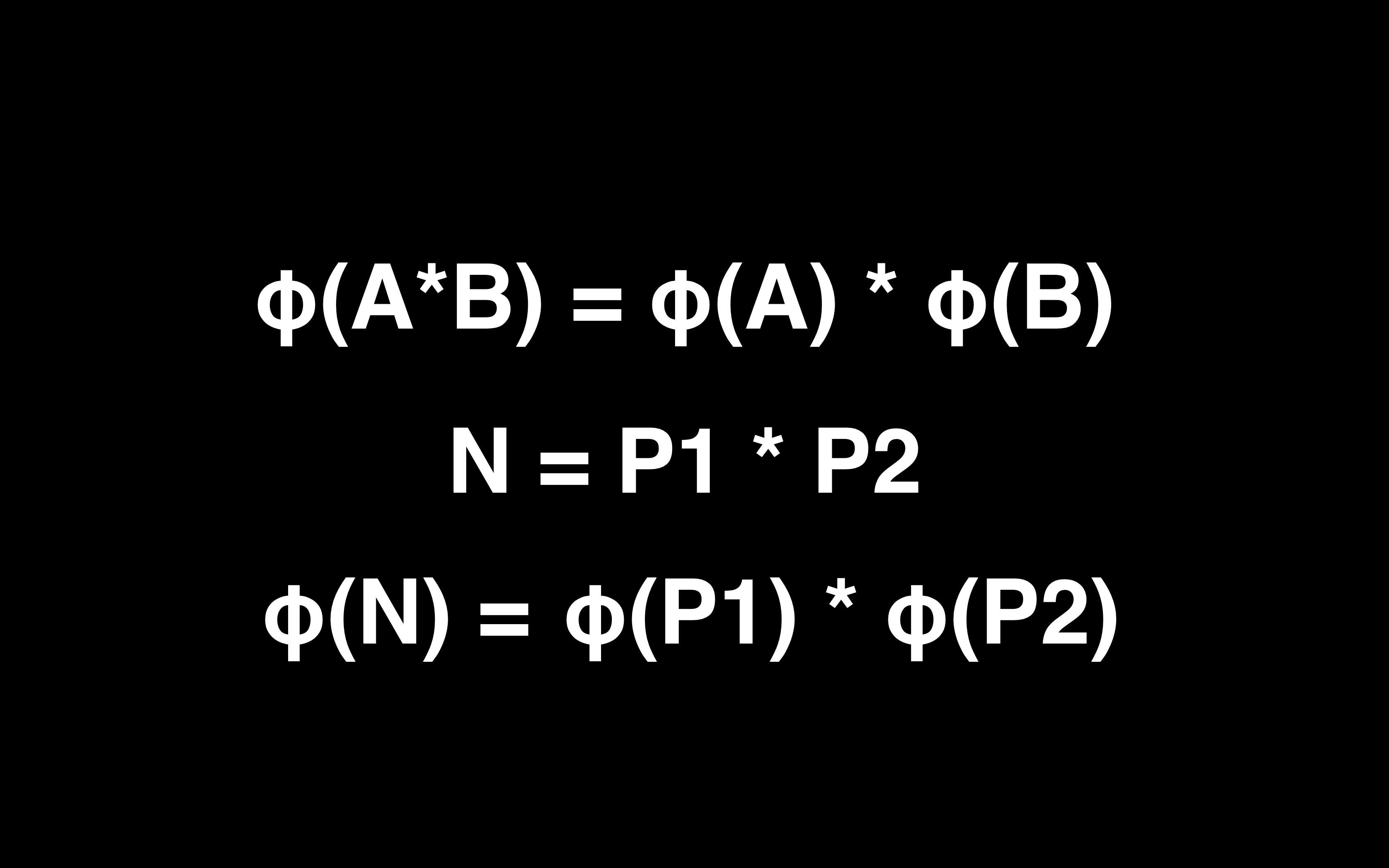现在我们有了求解 φ 函数的陷门，当我们知道了 N 的质因数分解时，求解 φ(N) 很容易
现在我们面临的新问题是如果将前面提到的模拟运算和 φ 函数结合起来
欧拉定理
为了解决新的问题，我们需要用到欧拉定理，也就是 φ 函数与模幂运算的关系如下，当 m 和 n 互素的时候，m 的 φ(n) 次方模 n 等于 1
下面我们需要引入两个规则：
① 1 的任何次方都等于 1，同理我们可以将 「m^φ(n) ≡ 1 mod n」的指数乘以任意的数 k，结果仍然是 1
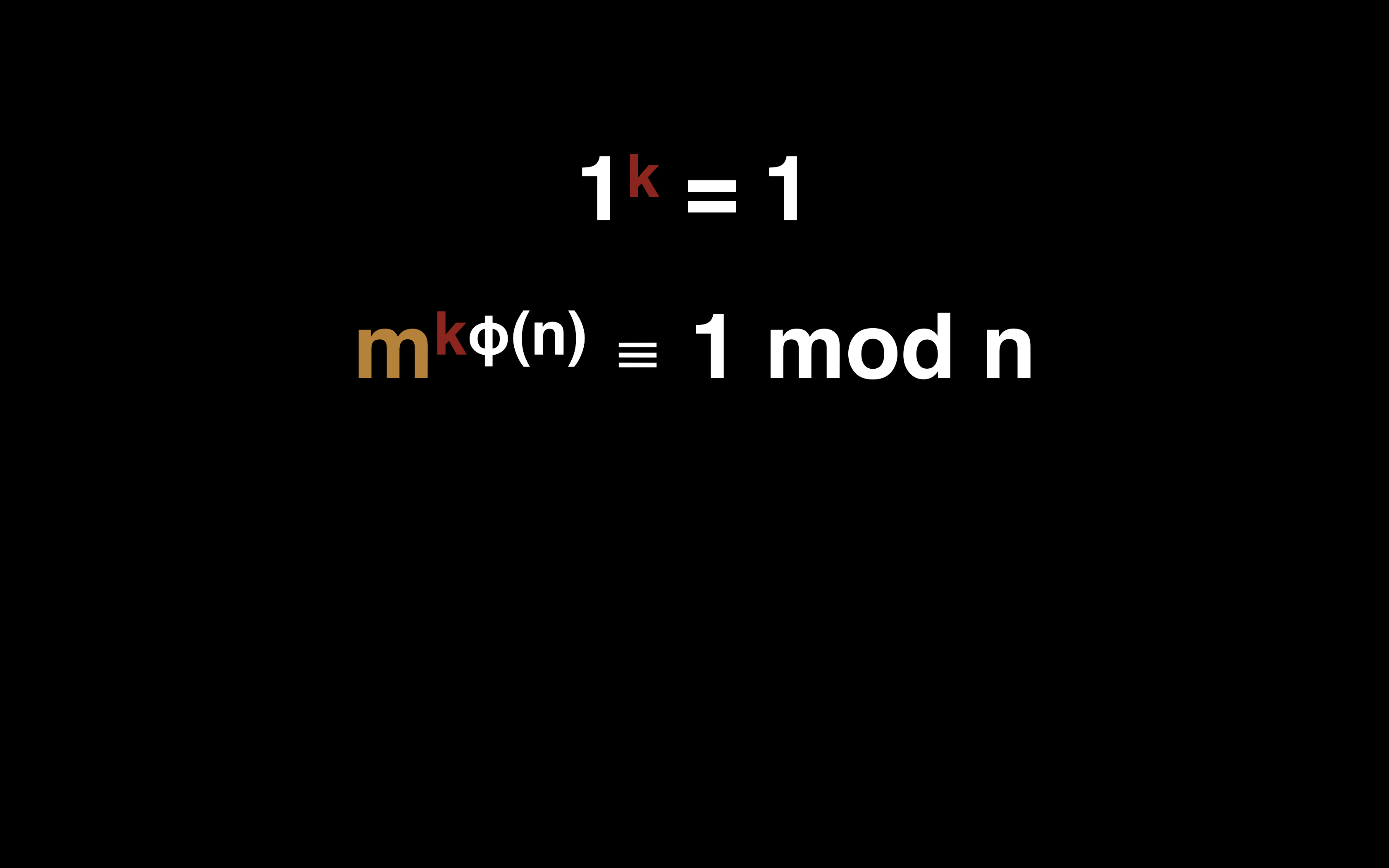② 1 乘以任何数 m 最后都会等于 m，同理我们可以将 「m^kφ(n) ≡ 1 mod n」的左侧乘以 m，右侧也会得到 m
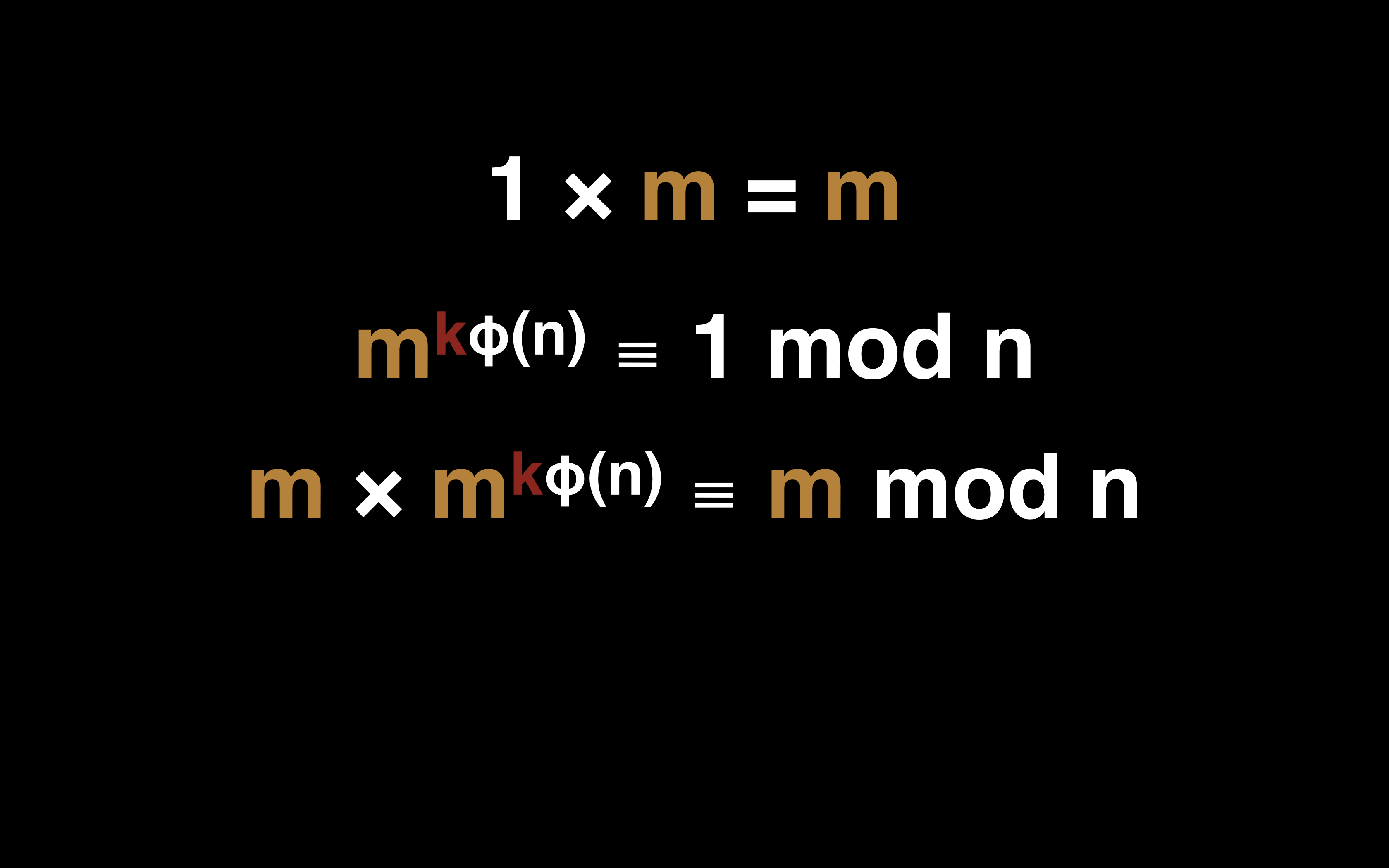将下面两个式子结合一下得到式子 m^1+kφ(n) ≡ 1 mod n：
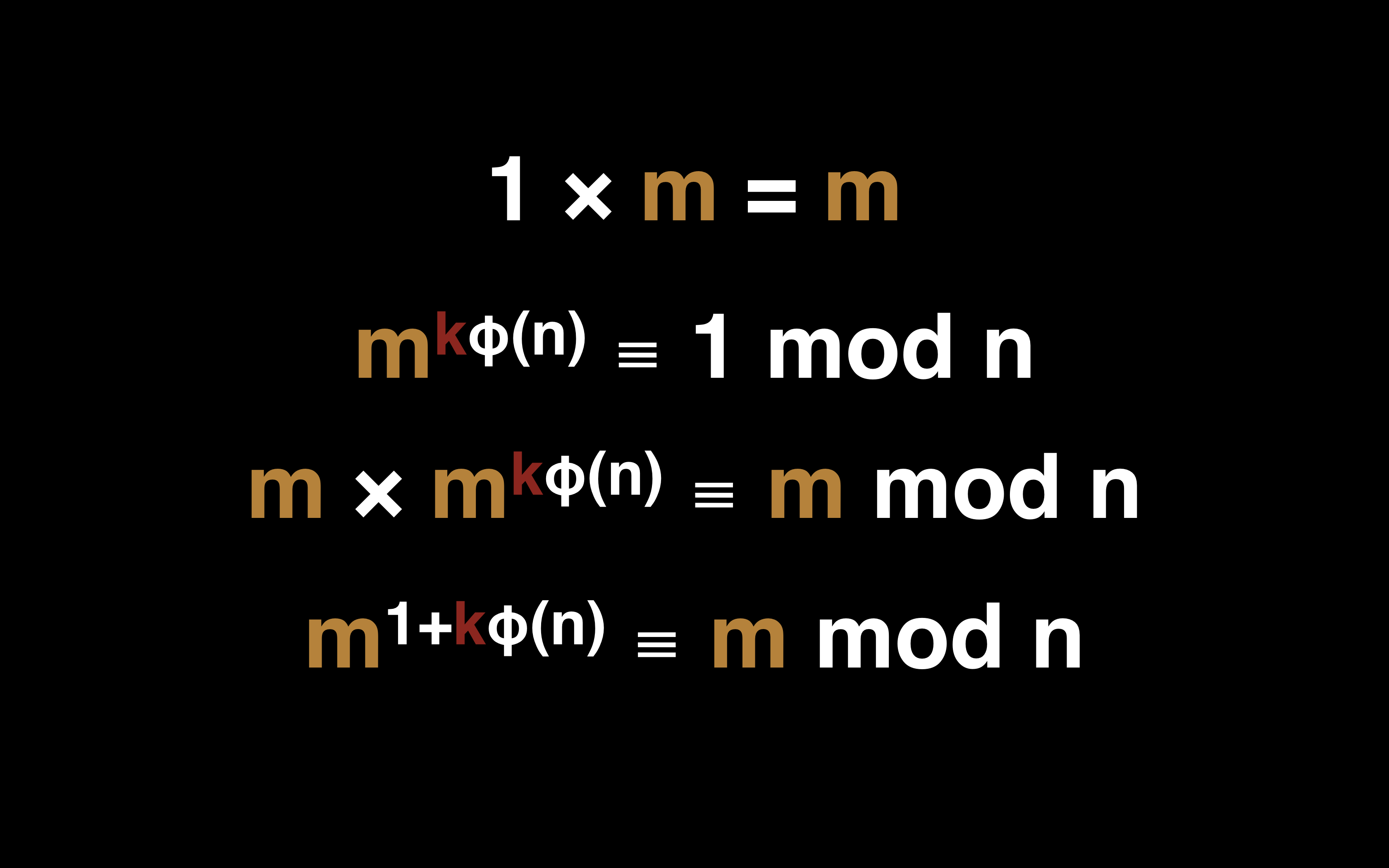还记得我们在前面一篇里面说到的目标吗？「找到 e 和 d 的关系，使得 m^ed ≡ m mod n」
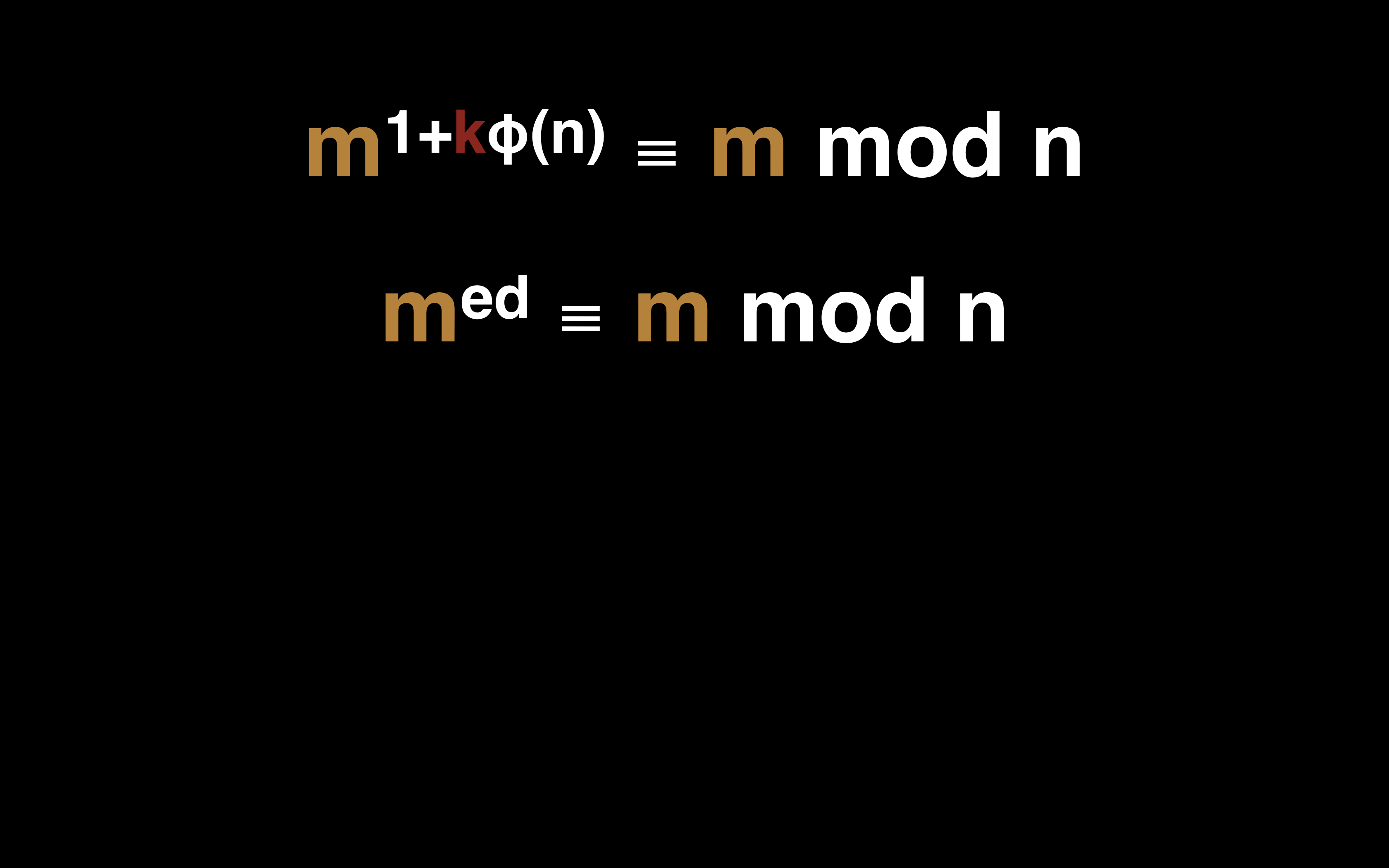其实我们已经得到了这个式子的结果了，也就是我们现在有了求 e 和 d 的等式：
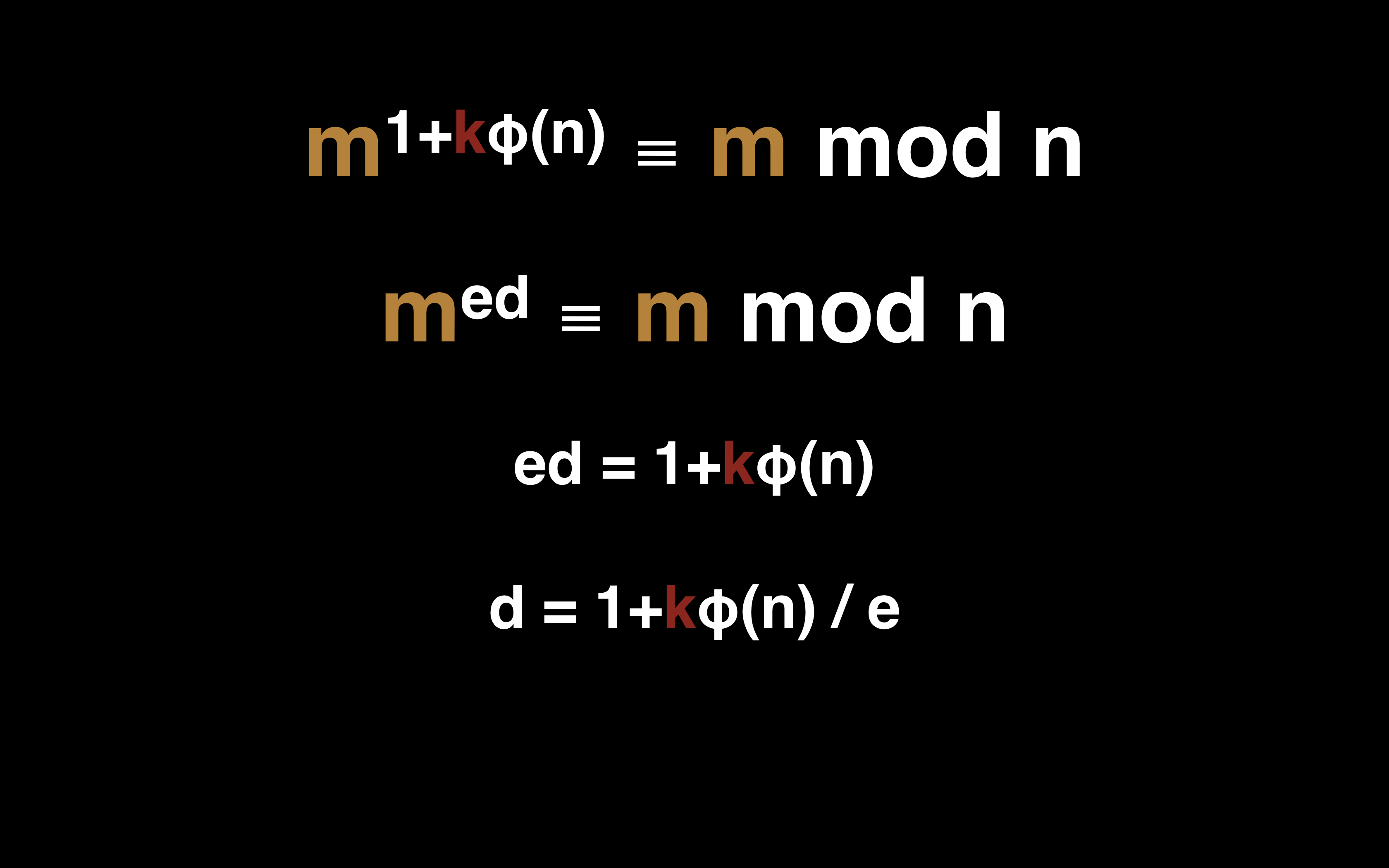
因为我们用到了 φ 函数，所以只有当我们知道 n 的质因数分解的时候计算 d 才容易，这里 d 就可以作为私钥了
例子
假设 Bob 有段信息数字化成了 m
① Alice 随机生成两个大小类似的随机质数 p1 和 p2，将两者相乘得到 n，然后就很容易可以算出 φ(n) = (p1 - 1) * (p2 - 1)，然后 Alice 选取一个小的公开指数 e，然后根据 φ(n) 和 e 求出 d 的值。到这里 Alice 为了保证绝对的安全需要将 p1、p2 和 φ(n) 销毁（生产环境中通常都是这么做的），并且妥善保存 d 的值
{n, e} 现在组成了 Alice 的公钥
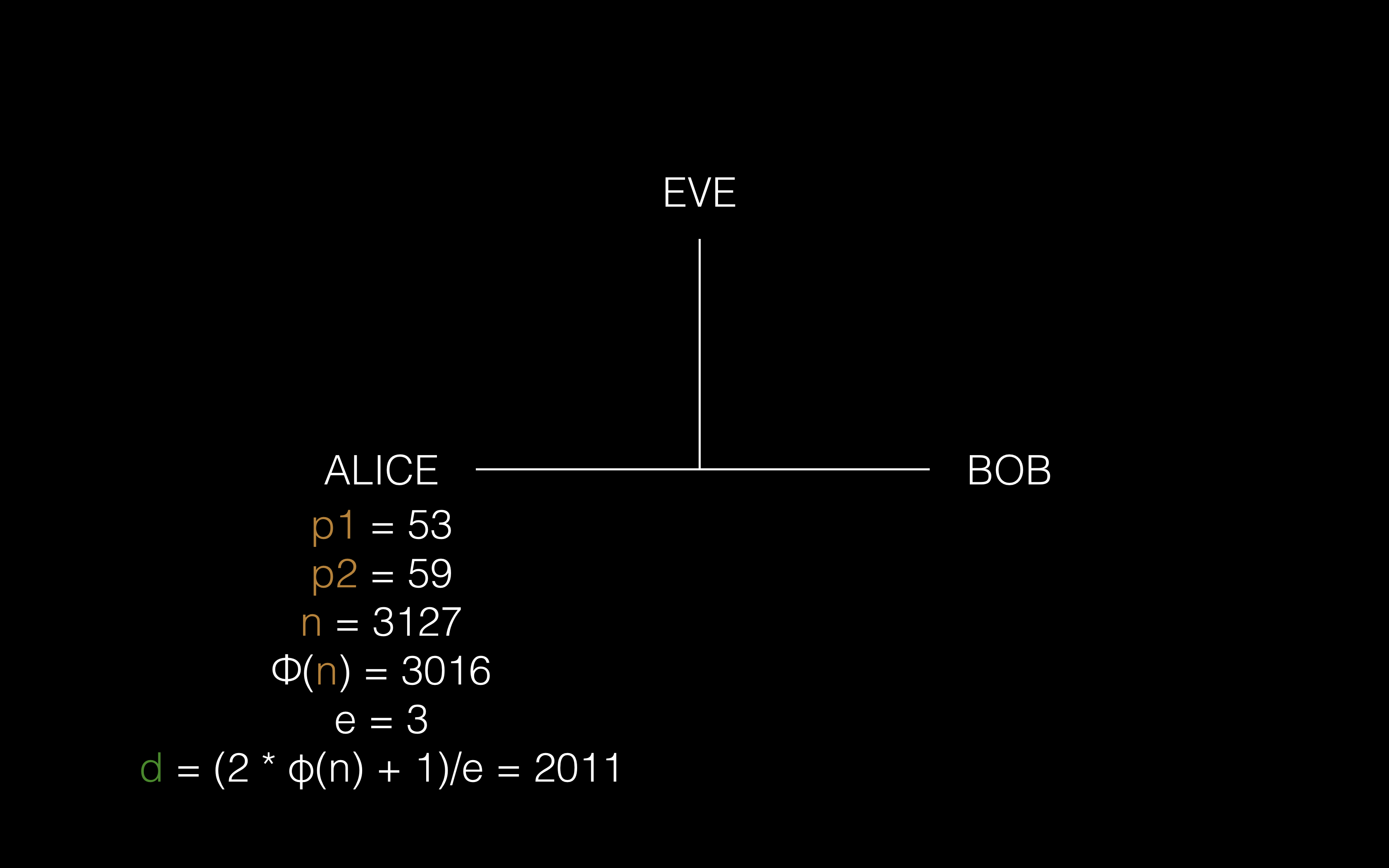
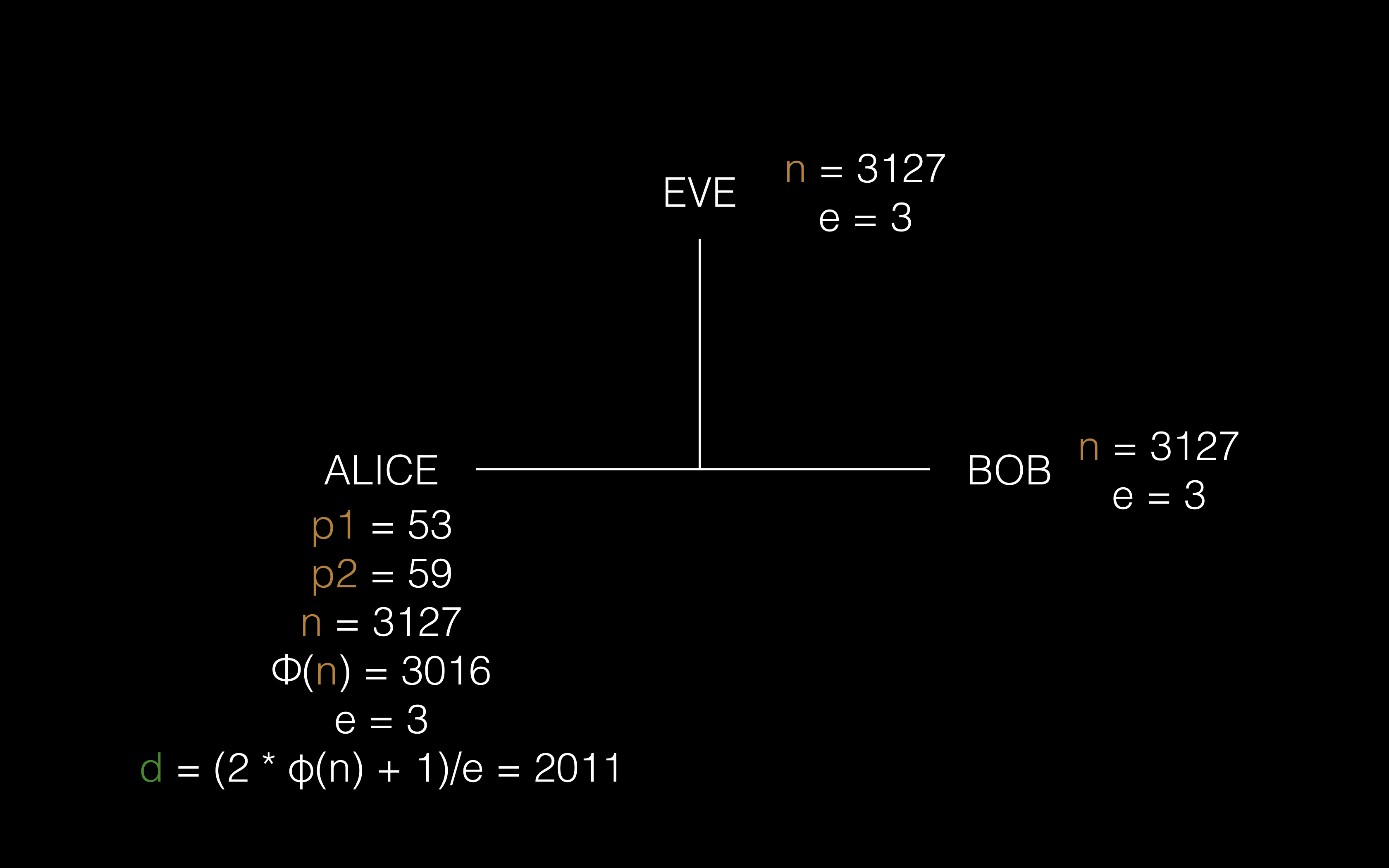
②Alice 将公钥发送给 Bob，让 Bob 可以用她的公钥上锁自己的信息，当然 Eve 是可以监听到的
③ Bob 计算 m^e mod n 得到加密信息 c
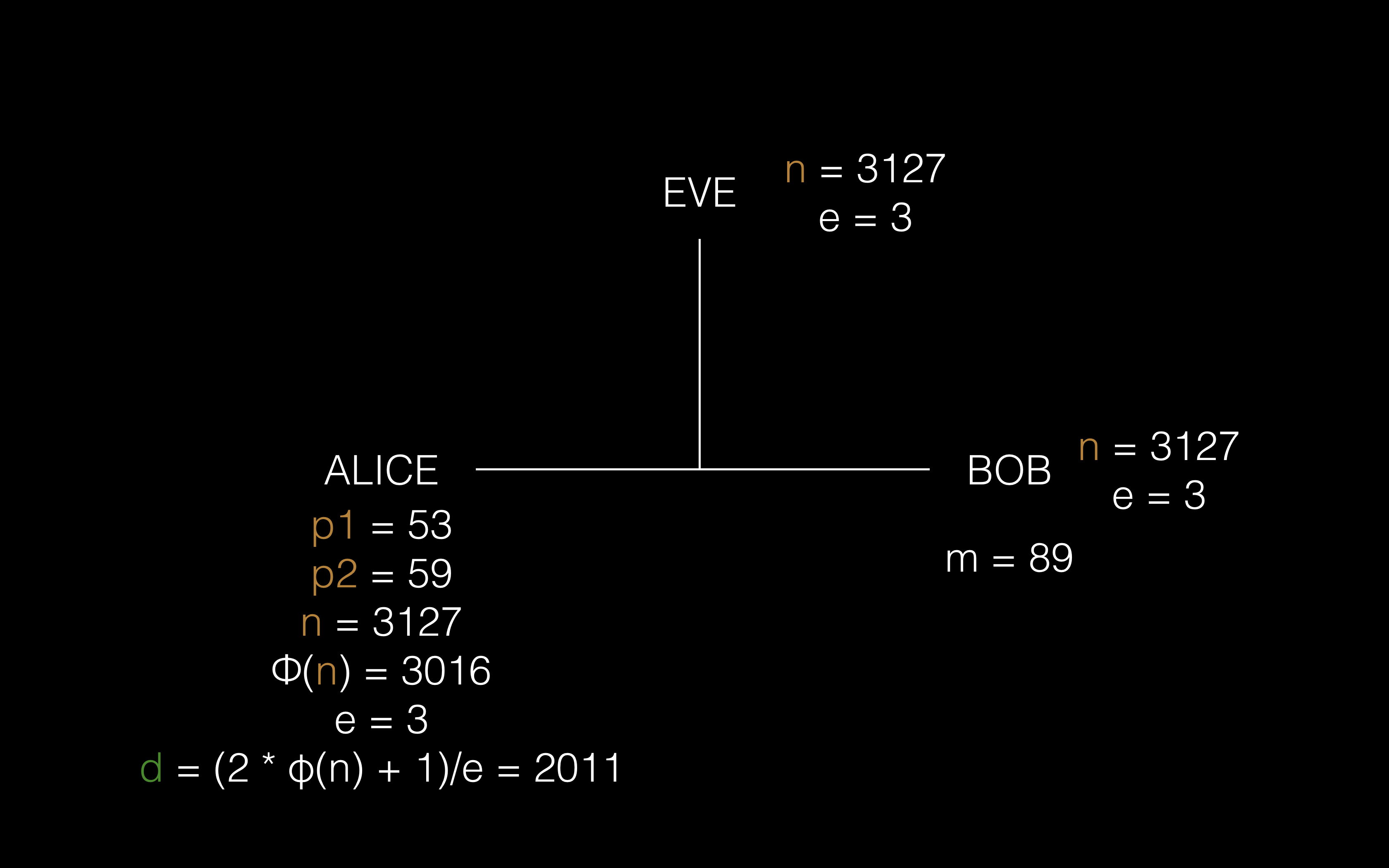
④ 将加密消息发给 Alice
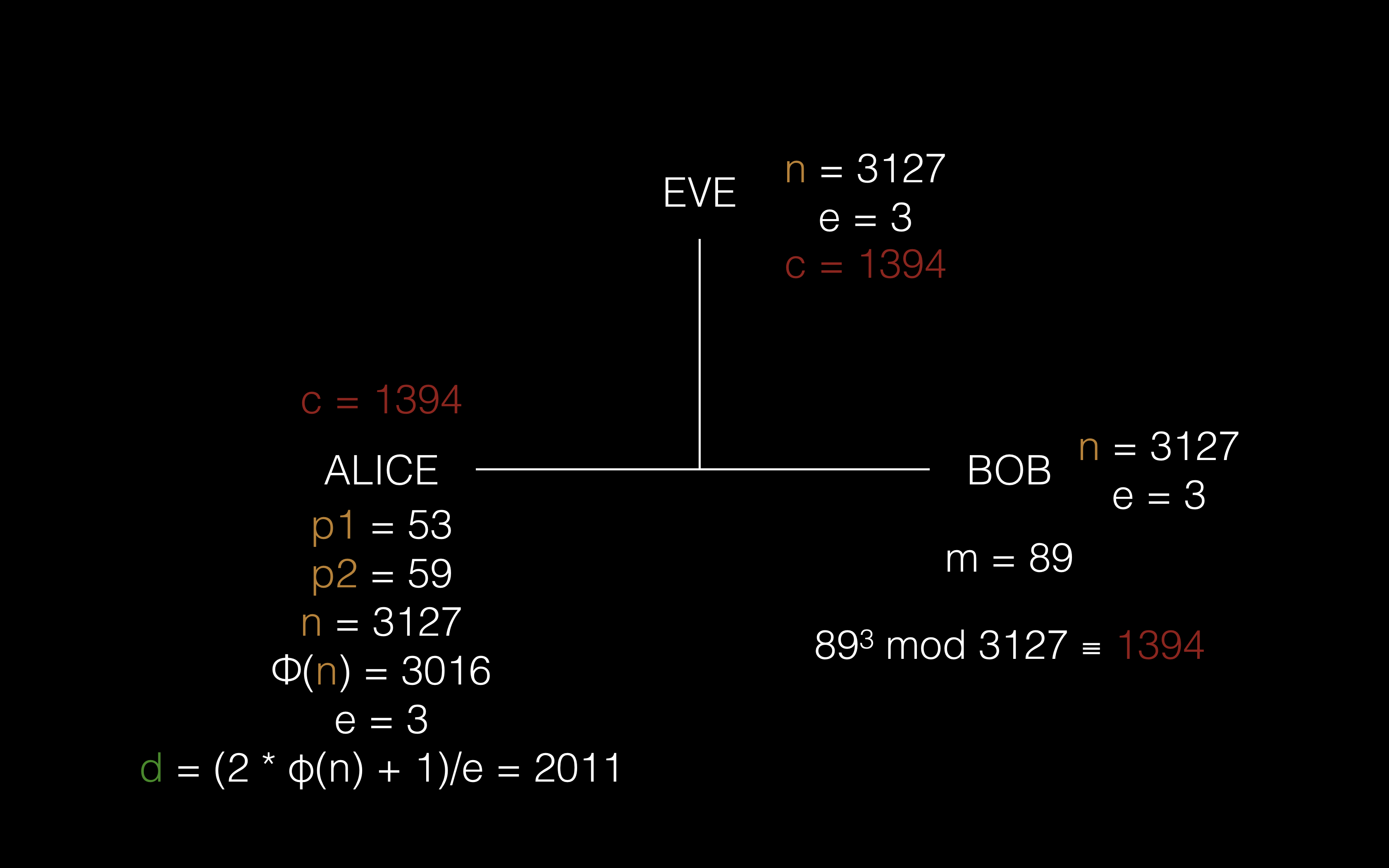
⑤ Alice 使用她的私钥 d 来解密这个信息，m = c^d mod n
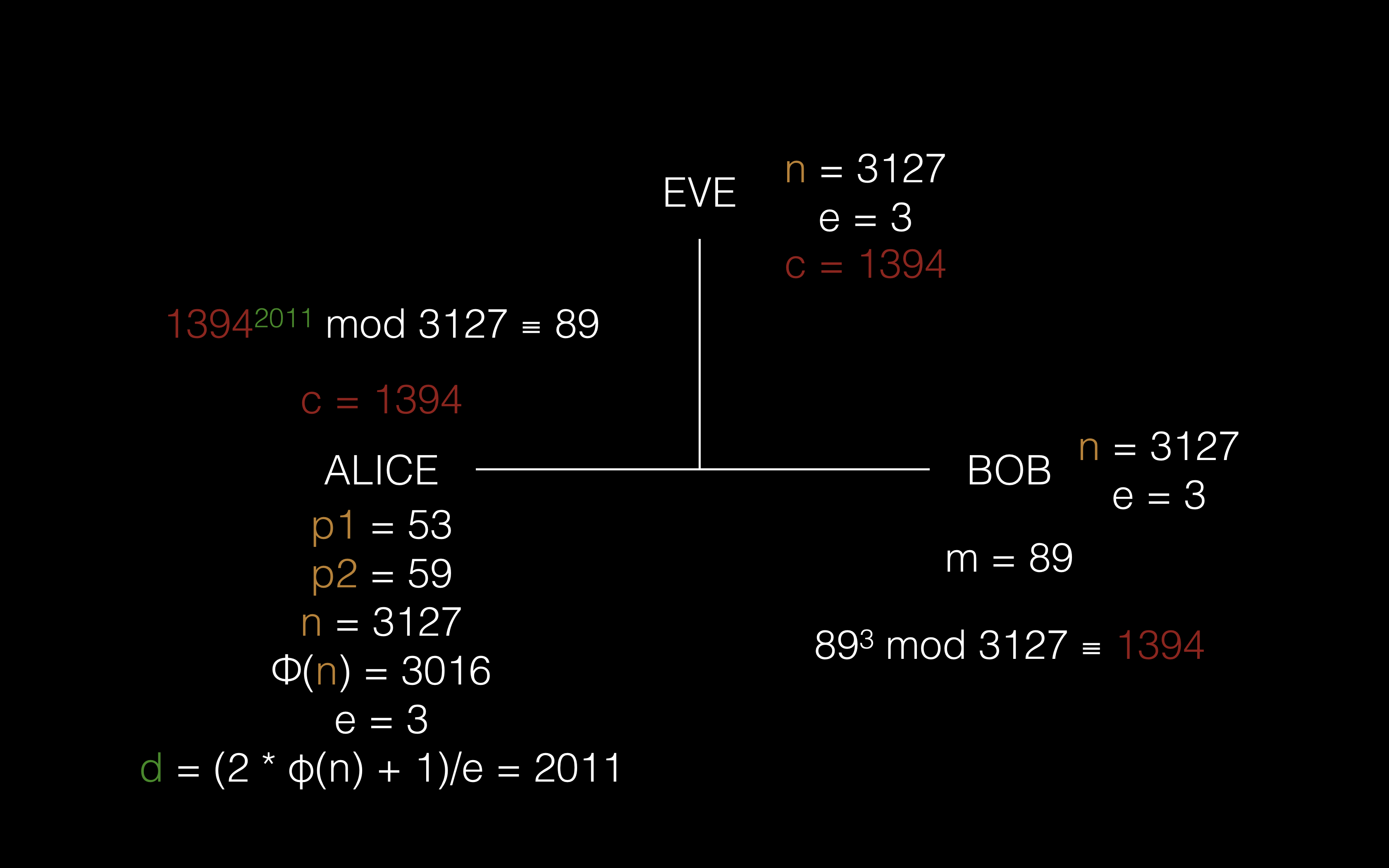
Eve 在整个过程中只知道 n、e、c， 想要求 m，必须知道 φ(n)，想要知道 φ(n) 就要知道 n 的质因数分解，当 n 足够大时，Alice 能够保证哪怕是最先进的计算机想计算出结果也需要数百年的时间，所以 RSA 整个过程的机密性就是这么保证的
其他
RSA 这套技术理论最初并不是由 RSA 三人发现的，只是他发布后立即被当做了国家机密，不过后来又被 RSA 这三个人独立的发现了 RSA 其实是依赖质因数分解这一困难问题的，其强度依赖于这一问题的困难程度 如果哪天人们找到了质因数分解的快捷方法，或者量子计算机发展使得暴力求解因数分解的问题可以控制在有限时间内，那么现有的非对称加密系统就完全不可用了