RSA 理论的正向思考过程（一）

之前写过一个从结论推导 RSA 正确性的数学正确性过程(RSA 算法正确性的证明)，比较生涩，现在来写写 RSA 理论的正向思考过程。

直到 1970 年代，密码学都是基于对称密钥的，就是加密解密密钥相同，所以 Alice 和 Bob 想要通信之前，先要共享密钥，但是如果 Alice 和 Bob 不能实际见面，那么密钥共享就很难保证安全，或者需要花费额外的通信开销来交换密钥，比如笛福赫尔曼密钥交换（之前写过此内容：笛福赫尔曼密钥交换 DH KEY EXCHANGE · YUI 的严肃文） 如果 Alice 是政府机构或者银行企业，需要和很多人通信，那么他在与人通信之前就需要花费大量的开销来和每个人协商密钥，并且还要储存管理大量的密钥。有没有方法可以解决这个问题呢？

NO KEYS ARE EXTENSION

1970 年一个英国工程师，试图实现公开密钥加密，这基于一种简单但是很巧妙的理论 ① Alice 拥有一把锁和对应的钥匙

② Alice 把打开的锁发动给 Bob

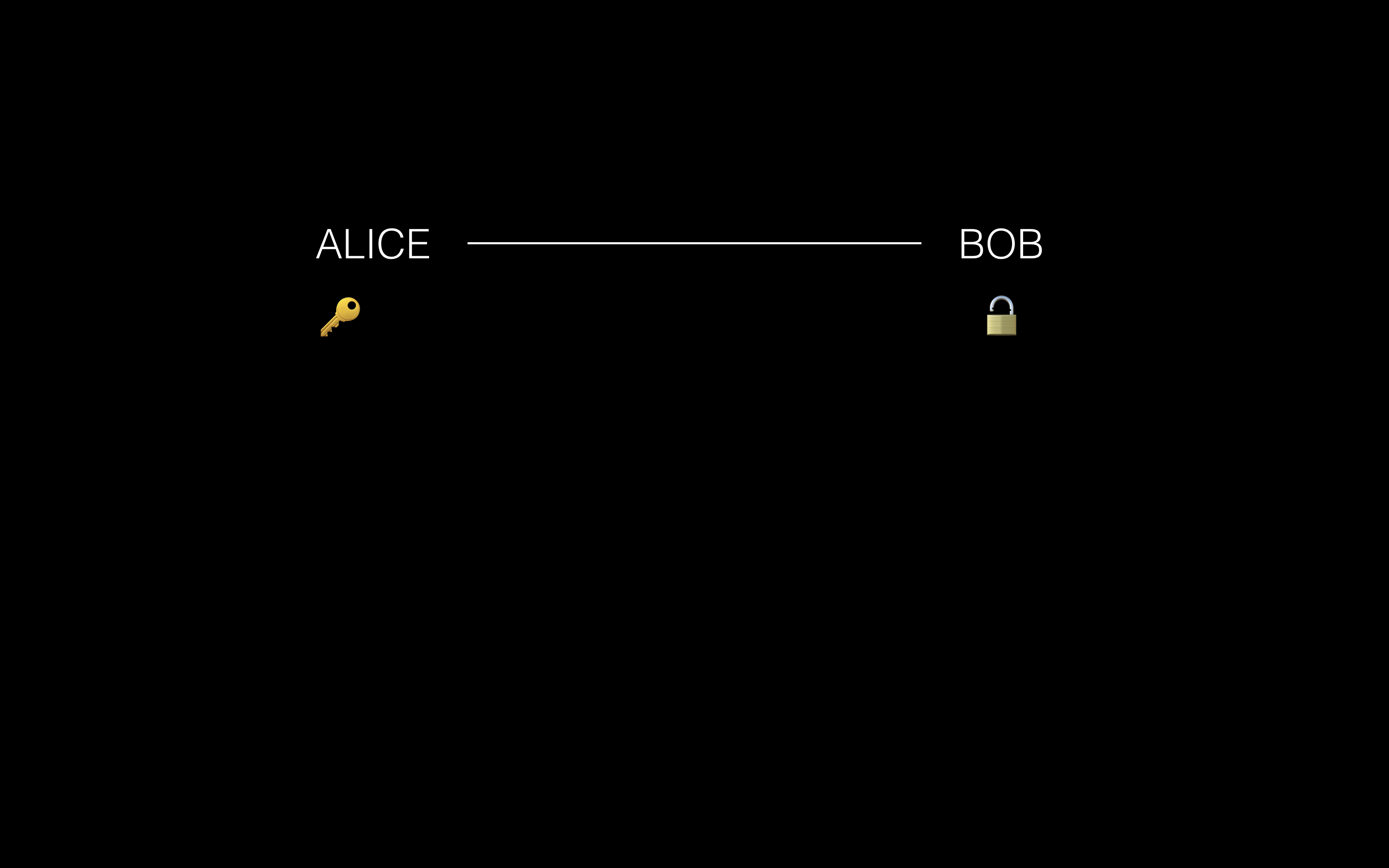
③ Bob 用这把锁给自己的信息加密，并将锁上的锁发送给 Alice

④ Alice 有对应的要是，所以成功解密

在整个过程中，可以发现锁可以给任何人使用，且钥匙是没有在通信信道里传输的。这就意味着锁可以公开，任何人都可以用锁发送信息，而这些信息只有alice能解读，而且 alice 只需要留有一把钥匙就可以和所有的人通信，听起来非常棒，这种思路的关键在于将密钥分为两个部分，一部分为加密密钥，一部分为解密密钥。但是提出这个概念的英国工程师没有找到相关的数学方法，最终这个问题由另一个英国科学家找到了解决方案

陷门单向函数

现在我们需要构造一种特殊的单向函数，叫做陷门单向函数（Trapdoor One-Way Function） 陷门单向函数首先是一种单向函数，也就是这种函数朝一个方向计算容易，但是反方向很难 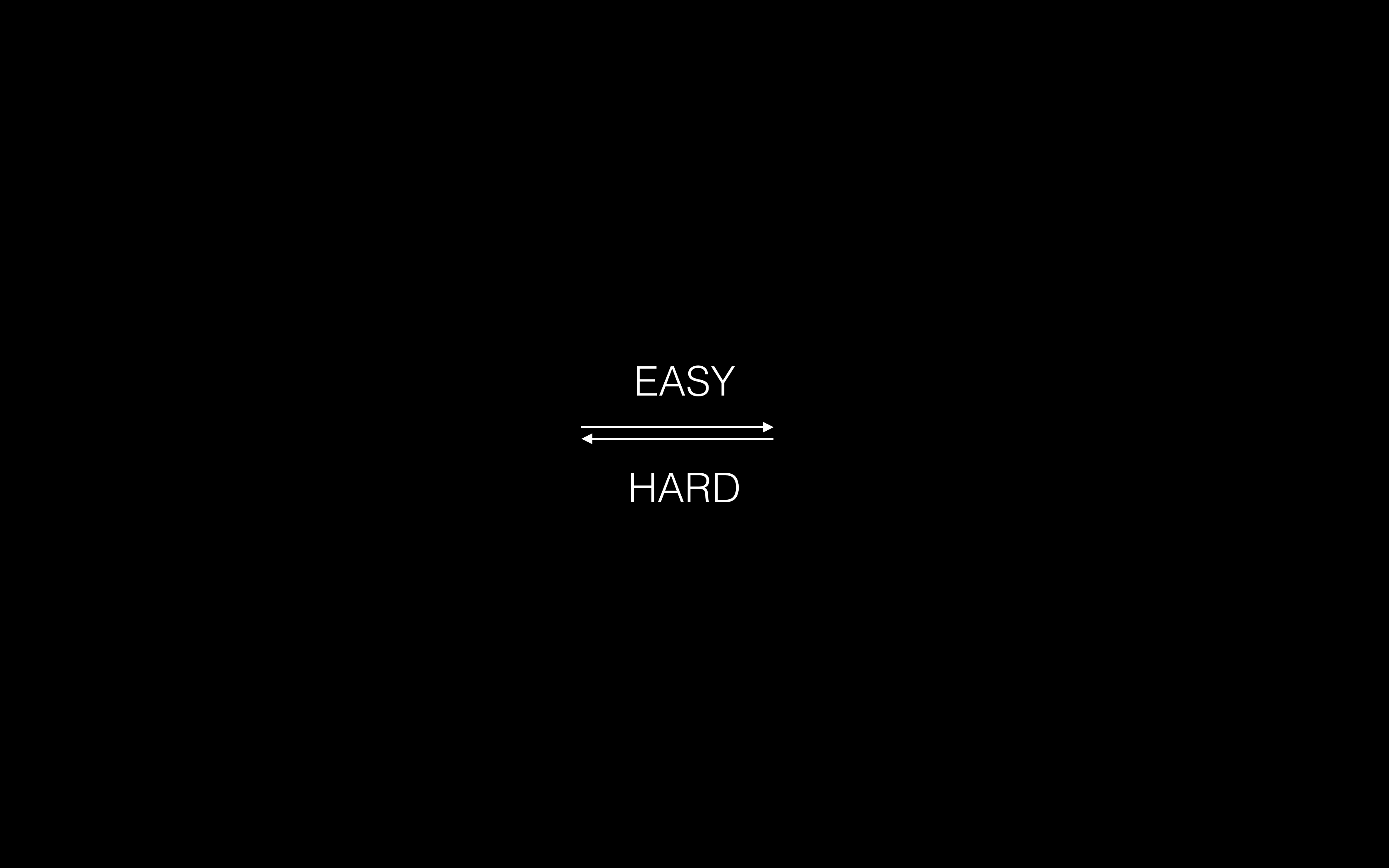但是如果你拥有一些关于陷门的特殊信息，那么反方向也变得容易，这种函数就称作陷门单向函数

模幂运算

那么我们想到了模幂运算，其过程用大白话来讲就是「取一个基数的某次方，除以质模数，输出余数」的过程

那么模幂运算可以被这样用于加密信息： 假设Bob 有一段信息被数字化成了m，他可以将数字自乘e次，这个e是公开指数，然后他可以将结果除以随机数 N，并输出除法的余数 这个计算过程很容易完成，但是反过来 知道 c、e、 n，求 m 很难 那么这个过程就是我们的数学锁，但是我们需要这把锁的钥匙，我们需要的钥匙其实就是前面提到的陷门，这是某种让解密过程变得很容易的信息 我们需要取 c 的其他次幂，比如 d 次幂，解除我们原来对于 m 所进行的运算，得到最初的信息 m 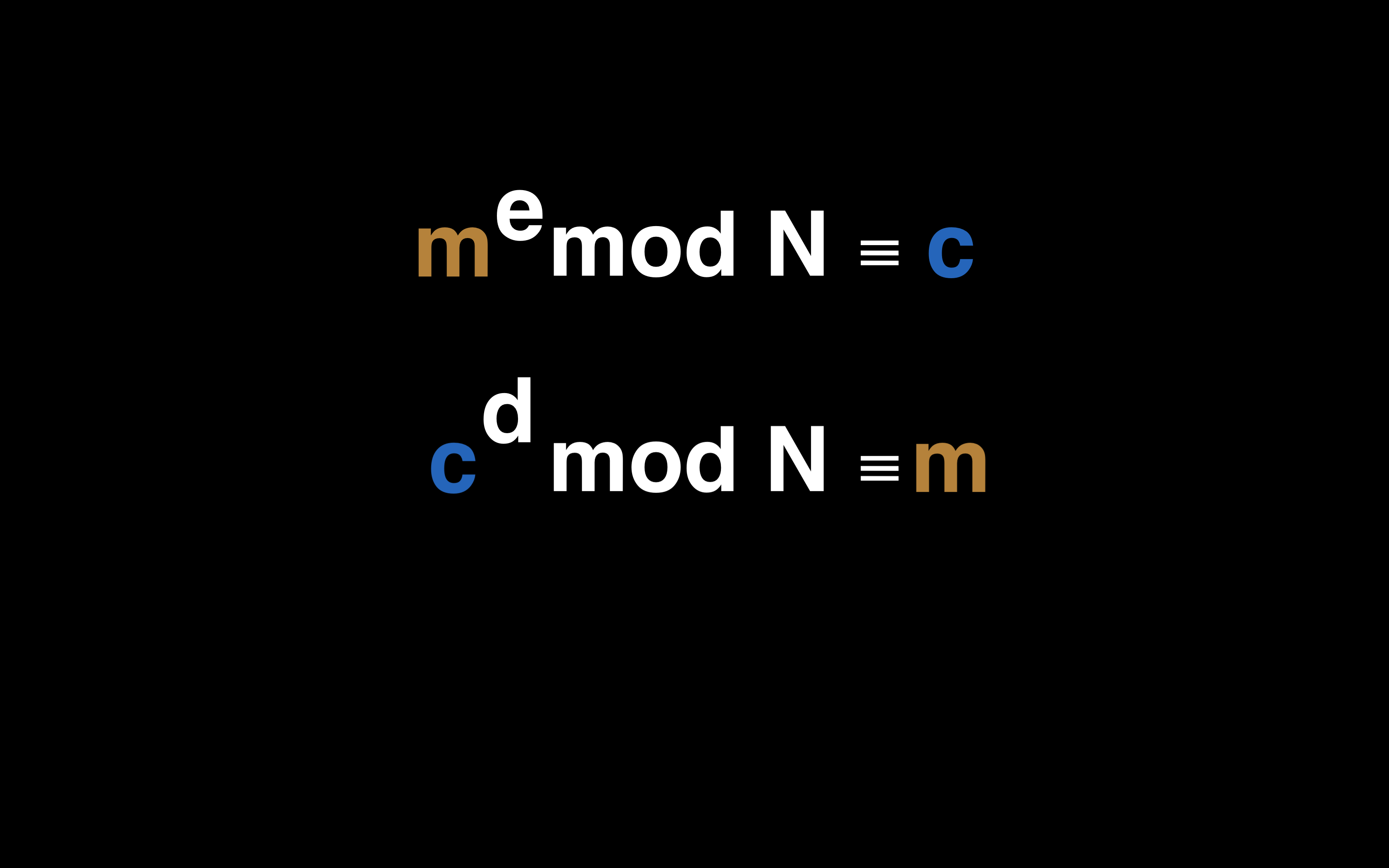把第一个式子的左边带入到第二个式子中 c 的位置，得到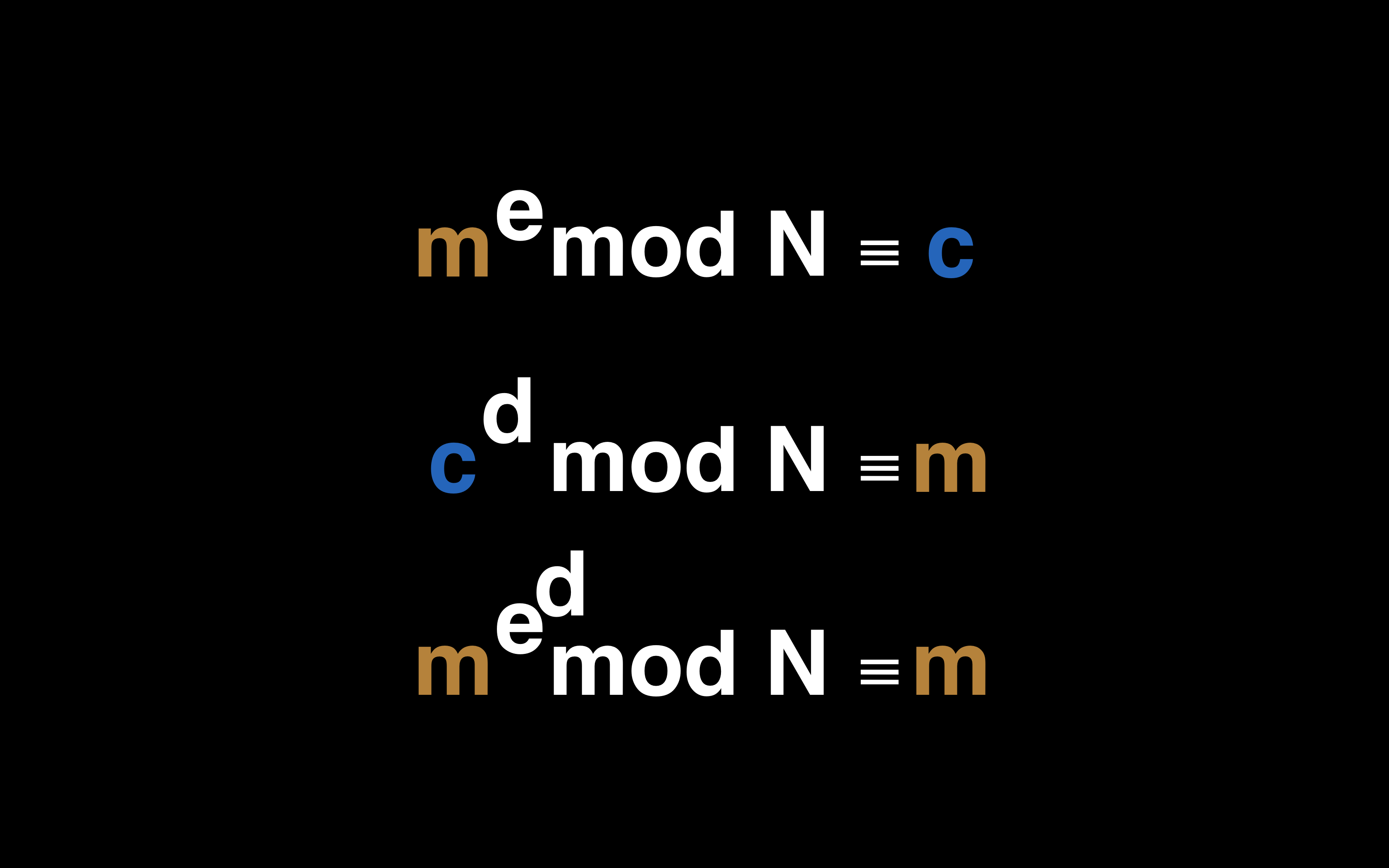： 最后也就是下面这个式子，e 表示加密密钥，d 表示解密密钥 于是，想要加密的人需要找到构造 e 和 d 的方法，导致很多人很难求出 d 的值，那么这就需要第二个单向函数用于生成 d 推导到现在，我们的现在的目标是：找到 e 和 d 的关系，使得 m^ed ≡ m mod n